Introduzione
L’argomento che vorrei trattare in questo mio primo articolo è un algoritmo di ricerca che mi ha incuriosito, la ricerca dicotomica (o ricerca binaria).

(Un algoritmo, non è altro che la strategia, un insieme finito di operazioni da effettuare per arrivare a risolvere un problema).

In linea di principio esistono diversi algoritmi di ricerca, a partire da quello lineare che concettualmente non è altro che lo scorrere una lista di elementi fino ad individuare l’oggetto cercato, fino ad arrivare ad algoritmi molto più complessi ed efficienti.
L’algoritmo di ricerca binaria si applica, necessariamente, su un insieme ordinato di elementi.
Cerchiamo la parola "Limone" su un dizionario.
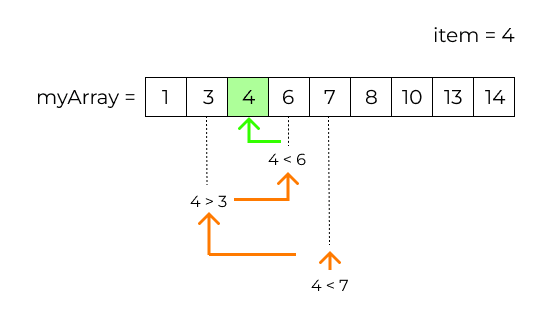
Il principio base è quello di evitare di cercare il nostro oggetto scorrendo tutti gli elementi del nostro insieme ma, per dimezzarne il tempo di ricerca, si aprirà il dizionario al centro, si individuerà l’insieme di parole contenute nell’ipotetico “centro” del dizionario e si deciderà, se le nostre pagine contengono la lettera “M” sapremo che dovremo cercare nella parte sinistra e non in quella di destra, si ripeterà l’operazione fino al raggiungimento della parola “Limone”, ma prendiamo un esempio grafico, analizziamo l'immagine sotto

Abbiamo un insieme di numeri ordinato, dobbiamo capire se il numero 4 è al suo interno, possiamo scorrere tutto l’array confrontando il numero 4 con ognuno degli elementi fino all’obiettivo, capirete che la ricerca può essere veloce in questo caso perché il 4 è il terzo numero, ma considerate un array di milioni di elementi e il vostro è alla fine……
Applichiamo la ricerca binaria. Calcoliamo la lunghezza del nostro array e dividiamo per 2 otteniamo che la metà cade sull’indice 4, che corrisponde al numero 7, è uguale al nostro numero?
No, è minore o maggiore? Minore, prendiamo in considerazione la metà sinistra.
Adesso l’array in considerazione partirà da 0 e finirà all’indice medio–1 , cioè [1,3,4,6]
dividiamolo a metà, il nostro numero è uguale al valore medio? NO, è maggiore o minore della metà? È maggiore, in questo caso allora spostiamo lo start, che varrà il valore medio+1, il nostro array risultante sarà composto da soli 2 elementi [4,6], dividiamo a metà, la mediana cade sul primo elemento, è uguale al numero ricercato? SI, abbiamo finito la ricerca!

Adesso trasformiamo questo algoritmo in codice.

function interactiveFunction(arr, x) {
  let start = 0;
  let end = arr.length - 1;
  //Il ciclo termina quando start è minore e/o uguale a end
  while (start <= end) {
    // Troviamo l’indice medio
    let mid = Math.floor((start + end) / 2);
    /* Se il valore contenuto nell’indice medio 
       è uguale al numero cercato ritorniamo True */
    if (arr[mid] === x) return true;
    /* Verifichiamo se valutare la parte destra o sinistra 
       dell'array */
    if (x < arr[mid]) {
      /* Se il numero cercato è minore del valore contenuto in  
         arr[mid] settiamo l’end al valore di mid -1 */
      end = mid - 1;
    } else {
      // Nel caso contrario aumentiamo lo start di 1
      start = mid + 1;
    }
  }
  // Se l’elemento non viene trovato ritorna -1 o false
  return false;
}

console.log(interactiveFunction([1, 3, 4, 6, 7, 8, 10, 13, 14], 10));

Questo metodo è interattivo, ma possiamo farlo anche con una funzione ricorsiva, accettiamo in ingresso 4 parametri, l’array, l’elemento che vogliamo trovare, l’indice inziale (default a 0), lunghezza dell’array (default la lunghezza iniziale)

function recursiveFunction(arr, item, start = 0, end = myArray.length - 1) {
  // Troviamo l’indice medio
  const middleIndex = Math.floor((start + end) / 2);
  // Verifichiamo se il valore è uguale al numero cercato
  if (item === arr[middleIndex]) {
    return true;
  }
  // Termina se l'elemento non viene trovato
  if (start >= end) {
    return false;
  }
  /* Se il numero ricercato è minore del valore medio
     richiamiamo la stessa funzione modificando il valore
     dell’end, in caso contrario modifichiamo lo start */
  return item < arr[middleIndex] 
     ? recursiveFunction(arr, item, start, middleIndex - 1) 
     : recursiveFunction(arr, item, middleIndex + 1, end);
}

//console.log(recursiveFunction([1, 3, 4, 6, 7, 8, 10, 13, 14], -4));

E questo è tutto, come primo articolo spero sia stato chiaro e comprensibile, aspetto feedback da parte vostra e spero sia stato utile.
Ciao!!