Continuing from the last post, Heap Part 01, I would explain heap sort which happens when inserting and deleting items from a heap. Let me recap from what I covered last time. We were doing a min-heap example and its basic methods such as parent(), left_child(), right_child().

Learning algorithms - Heap | part 01

Jenny Yang ・ Oct 18 ・ 4 min read

#computerscience #algorithms #heap #datastructures

Violation

Violation in a heap is when a child node is greater than a parent node in max-heap or child node is less than a parent node in min-heap.

Insertion

We are going to have a look a trivial example of how items inserted, to understand the heap sort. To start with, we are going to insert 7, 1, 3 in the order.

insert(7)
insert(3)
insert(1)

Did you notice? every time we inserted an item, there will be a comparison of two items, a parent and child, and swap the two when there is a violation. Continuing inserting items from the given example.

insert(20)
insert(11)
insert(9)

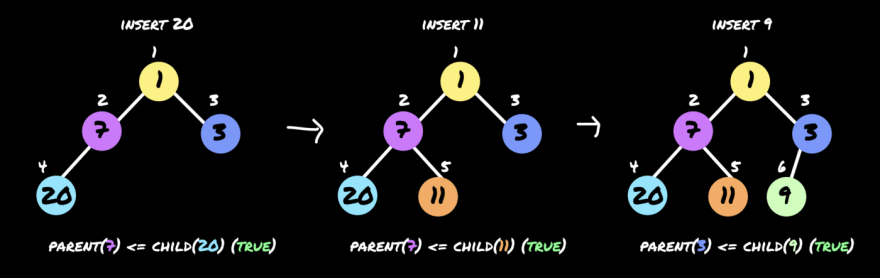
We inserted 7, 3, 1, 20, 11 and 9 so far. There has not been any swap in the second round. Moving on to the next round.

insert(3)
insert(15)
insert(4)
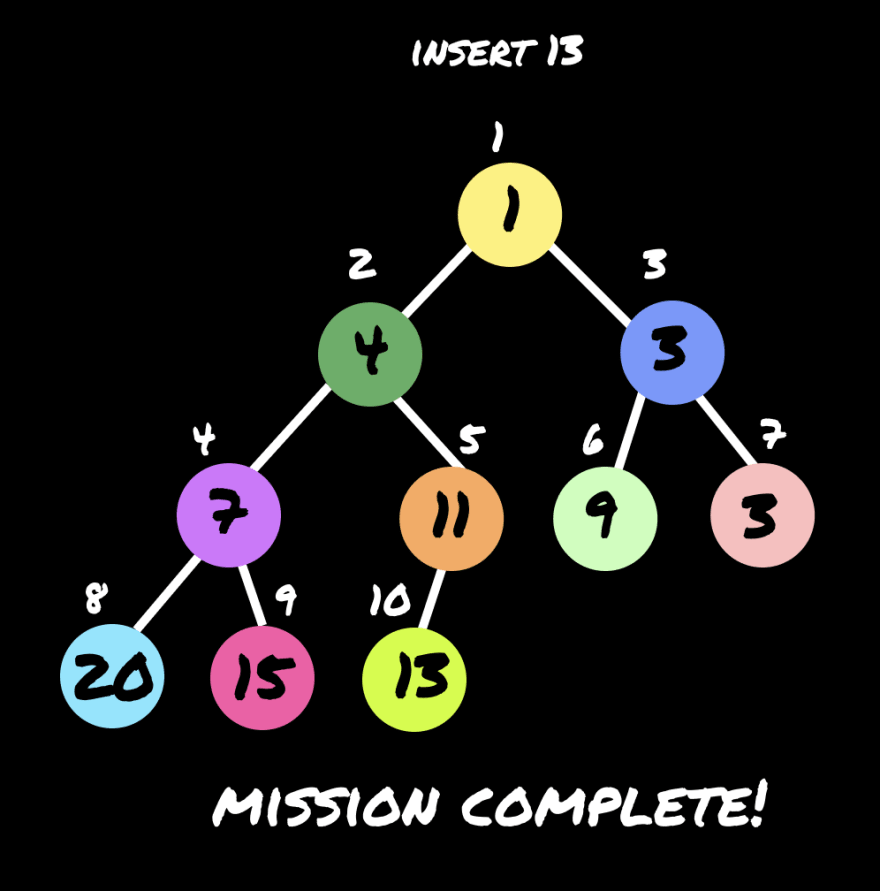
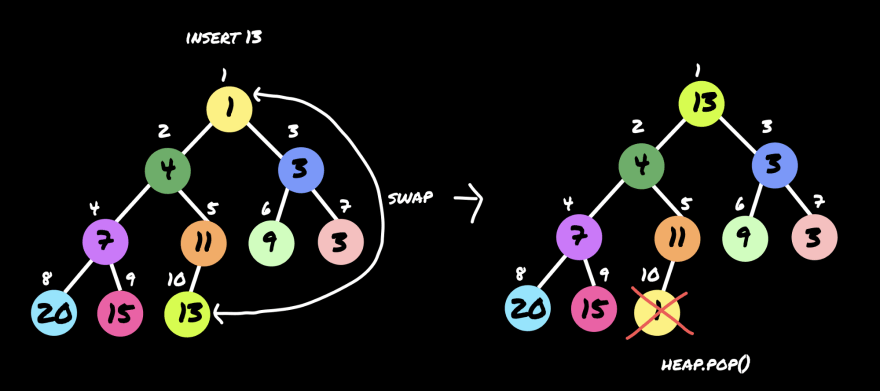
insert(13)

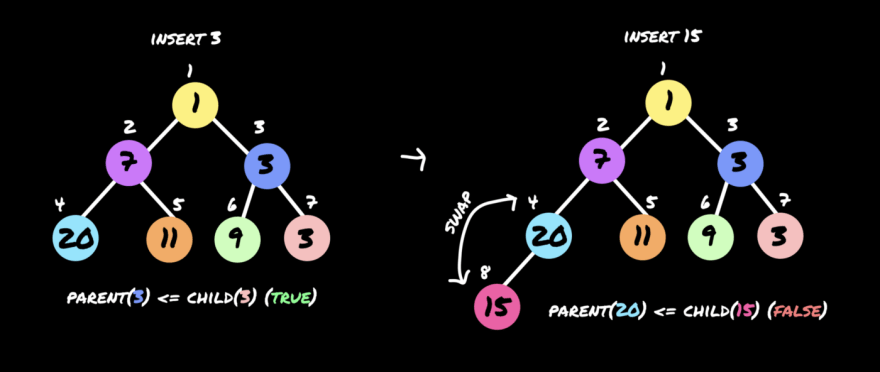
We swapped 20 and 15 as 15 is smaller than its parent 20, and moving on to parent node 7, the parent 7 is smaller than its child 15, so it is all sorted.

There are two comparisons 4 and 15, 4 and 7, the number 4 initially inserted in [9] and moved up to [2] as it is swapped with its parent each time. Last round is to insert 13, hang in there till the end.

Final result

Extract min

Extract min is the deletion method in a heap. In a big picture, there are two steps:

1. deletion: swap [1] and [n] where n = length of a heap exclude [0] and delete the [n] which is the min item.
2. heap sort: swap until the item in [1] is smaller than its children.

step 1: deletion

step 2: heap sort

Swap

Swap method is simply swapping two items and will be used in heapify() method.

def swap(self, a, b):
    self.heap[a], self.heap[b] = self.heap[b], self.heap[a]

Heapify

Whenever there is a violation in heap properties, we are going to correct the violation by swapping a child and a parent. What I mean by violation is, when a child is less than its parent in min-heap. There would be two ways of implementation using recursion or iteration. Insertion and deletion always run heapify at the end of the execution to keep to sort the heap.

Iteration

def heapify(self, i):
    parent = i // 2
    """ 
    as long as the element is in the range of index of a heap 
    (0 is not included)
    """
    while i // 2 > 0:
        # if the element is bigger than its parent swap them
        if self.heap[i] < self.heap[parent]:
            self.swap(parent, i)

        # move the index to the parent
        i = i // 2

Let me break down the code line by line.

1. while i // 2 means as long as the in the range (from 1 to n)
2. self.heap[i] < self.heap[parent] if the current node is less than its parent, swap those two since parent should be smaller.
3. i = i // 2 means bubble up to its parent to keep checking the violation.

Note: i in this heapify is self.size which refers to the last index

Recursion

def heapify(self, i):
    l = self.left(i)
    r = self.right(i)
    smallest = i

    """
    if the r and l are within the range of index,
        and if one of those are smaller than i,
        swap them with i
    """
    if l <= self.size and self.heap[l] < self.heap[i]:
        smallest = l
        print(f"now smallest is {self.heap[l]}")
        self.swap(i, smallest)
    if r <= self.size and self.heap[r] < self.heap[i]:
        smallest = r
        self.swap(i, smallest)

    """
    recursively do the process(heapify) above
    until i becomes smallest in the three relationships in the tree
    """
    if smallest != i:
        self.heapify(i)

Break down:

i = parent node
there are three pointers that refer to the left child, right child and smallest. In here, the important thing to remember in here i ≤ l or r.
if l or r are within the range of index and one of those are smaller than i, then swap them with i since i should be the smallest.

1. recursively do the process until i becomes smallest amongst the three (left child, right child, parent i).

Implementation

The two insertions are basically the same, the argument the heapify method receives varies due to different heapify method. Firstly, appending a new node then increase size. Lastly, sorting the heap.

Insertion: iteration

def insert(self, key):
    self.heap.append(key)
    self.size += 1
    # Fix violation if there is one
    # iteration heapify
    self.heapify(self.size)

In iterative insertion, the heapify takes the last index.

Insertion: recursion

def insert(self, key):
    self.heap.append(key)
    self.size += 1
    # Fix violation if there is one
    # recursion heapify
    self.heapify(self.size // 2)

In recursive insertion, the heapify takes the parent index of the last item.

The time complexity of insertion is appending O(1) + size alteration O(1) + heapify O(log n) = O(log n)

Deletion (extract min)

Code break down:

1. store the item to delete
2. swap the root item with the last one
3. delete the last item that where there is min item
4. heap sort until it meets the criteria
5. return the removed item

def extract_min(self):
    popped = self.heap[1]
    # swap last item and the root(min) item
    self.swap(self.size, 1)
    # pop the last item off
    self.heap.pop()
    # reduce size of the heap as an item is deleted
    self.size -= 1
    # sort the heap
    self.heapify(1)
    # return the popped item
    return popped

Easy peasy, yeah?

The time complexity of deletion is swap O(1) + deletion O(1) + size alteration O(1) + heapify O(log n) = O(log n)

Time analysis

Heapify plays a key role in this algorithm. Because other steps in insertion and deletion are constant time, what we really care about is the heapify method. Let me explain why heapify takes logarithmic time.

If N = 9, the heapify will take a maximum of 4 steps in the worst case, therefore the height of the tree would be the time to process the heapify function. Let's substitute the N to logarithm formula.

2³ is roughly equal to 9, hence the heapify is O(log N)

I still have one advanced method to explain. I will see you in part 3!