This is a leetcode question found in the May Challenge week 3.It's a medium level question, and I could only think of the brute force recursive solution(which obviously led to exceed the time limit). So I checked the discussion forum and found a beautiful dynamic programming solution, which I was determined to understand!Here I'm going to give you some intuition about the answer through a series of ugly but helpful drawings. I hope it helps!

Here's the link to the discussion, this solution is by Lee215: https://leetcode.com/problems/count-square-submatrices-with-all-ones/discuss/441306/JavaC%2B%2BPython-DP-solution
So if you didn't check the link, here is the solution and the provided explanation for it:
"dp[i][j] means the size of biggest square with A[i][j] as bottom-right corner.
dp[i][j] also means the number of squares with A[i][j] as bottom-right corner.

If A[i][j] == 0, no possible square.
If A[i][j] == 1,
we compare the size of square dp[i-1][j-1], dp[i-1][j] and dp[i][j-1].
min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1 is the maximum size of square that we can find."

   public int countSquares(int[][] A) {
        int res = 0;
        for (int i = 0; i < A.length; ++i) {
            for (int j = 0; j < A[0].length; ++j) {
                if (A[i][j] > 0 && i > 0 && j > 0) {
                    A[i][j] = Math.min(A[i - 1][j - 1], Math.min(A[i - 1][j], A[i][j - 1])) + 1;
                }
                res += A[i][j];
            }
        }
        return res;
    }

So the second sentence in the discussion forum's explanation says "dp[i][j] means the number of squares with A[i][j] as bottom-right corner." So we will loop on every element with indices i,j and we will calculate the number of squares that have this particular element as it's bottom right element. The element could participate in many squares of different sizes, starting from a square of size 1 (just this element) up to the maximum size of squares possible.

The first sentence says "dp[i][j] means the size of biggest square with A[i][j] as bottom-right corner." So if I calculate the number of different squares that have this element as it's bottom right corner element, therefore this is also considered the maximum size square this element can participate in.

Now the question bubbles down to: How do I calculate the maximum square size a particular element can be in it's bottom right corner?

consider this matrix, where we are evaluating the element at index [1][1]'the element in a pink box', It is clear that the maximum square this element forms as the bottom right corner is a square of size 1, because element[0][0] is equal to zero. If element[0][0] was equal to one, then we could have combined the four squares of size 1 to create a new square of size 2x2, with element[1][1] as it's bottom right corner element. Remember that dynamic programming is all about breaking the larger problem into smaller problems.

Notice how this algorithm updates the matrix in place:
for all elements that have an index of value 0 (first row and first column values) These elements can only be the bottom right corner of squares of size 1, therefore we don't enter the if condition for these elements, we just add their value to "res" which is either 0 or 1.
for any other element with a value of 1, there is a potential for this element to be the bottom right corner of a bigger square, therefor we do this process to check: we get the minimum value for the left, upper left and upper elements from our current element we are processing. More formally we will get the minimum value for the squares that elements A[i - 1][j], A[i][j - 1] and A[i - 1][j - 1] form the right corner values for. Once we get the minimum value that means each of these smaller squares can be combined with the current element we are processing to form a new square bigger than the smaller squares by 1 row and 1 column.

Let's look at the combination process, here we have a matrix of all ones:

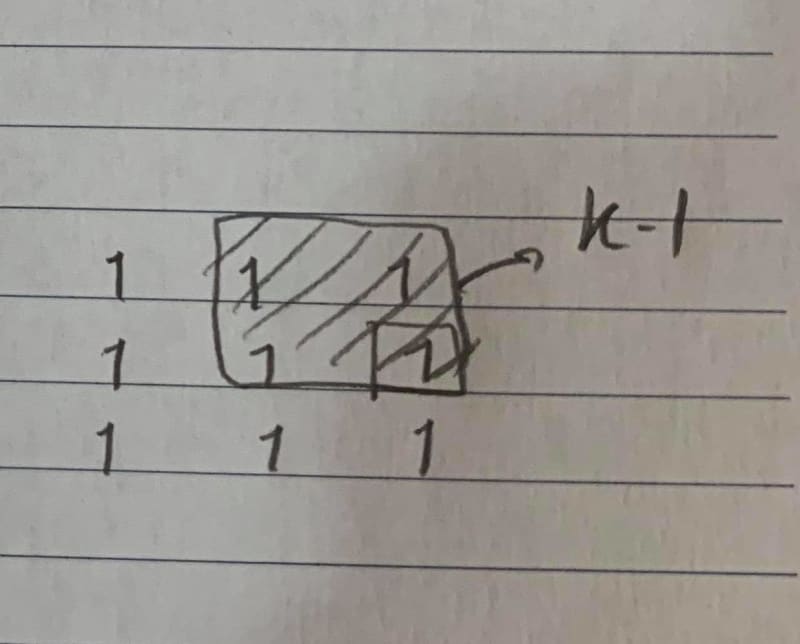
Look at element A[2][[2], it's obvious that the maximum square that this element forms it's bottom right corner is of size 3x3. How can we calculate this when we reach this element? We will have to see the previously calculated values in the left, upper left and upper elements. Here I have the 2x2 square shaded, which has element A[1][2] as it's bottom right corner. By the time we are processing element A[2][2], element A[1][2] will have the value of the maximum square that has A[1][2] as it's bottom right corner (which is 2).

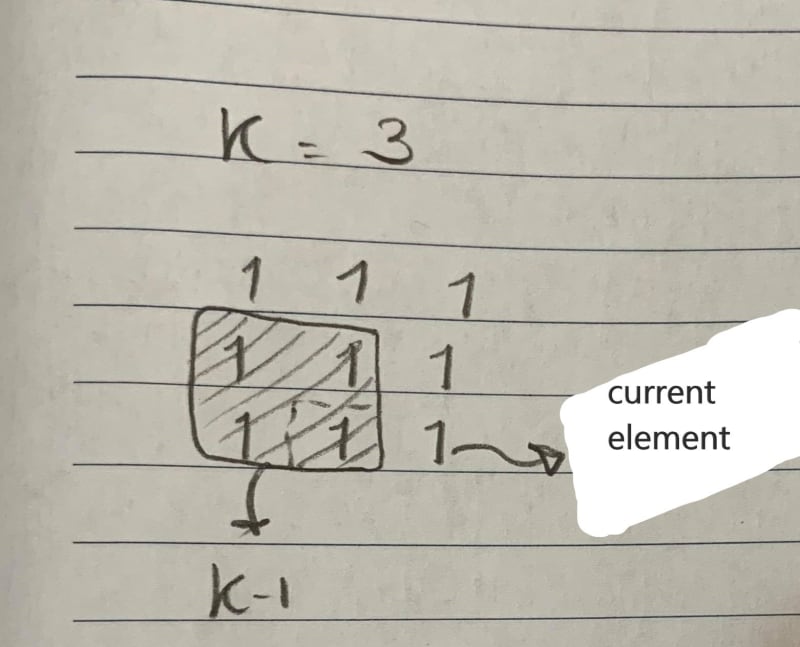
We are still processing the same element, but now we are looking at a different neighboring element, element[2][1], which is also the bottom right corner of a square of size 2.

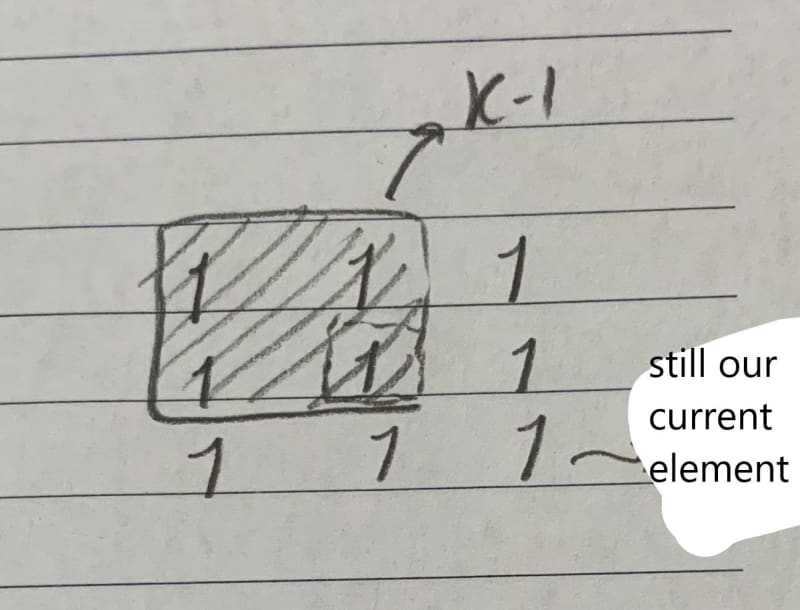
Here we are looking at our last neighbor at position [1][1], which is also part of a 2x2 square. All the neighbor elements are parts of squares of size 2x2. Therefore we can safely "combine" these 2x2 squares to form a larger square of size 3x3 with element [2][2] as it's bottom right corner element.

I hope this made the intuition behind the dynamic programming solution more clear. Keep on practicing problems and Good Luck!