Introduction

In my very first post we went through solving Rock, Paper, Scissors game using a 'mathematical' approach, and that entry ended with an open question:

Can you find a similar, mathematical approach for Rock, Paper, Scissors, Lizard, Spock?

I invested no time at all in thinking about this variant until a few days ago, when @jotagarciaz asked that same question to me and sparked my curiosity.

Game analysis: "Lizard, Spock" or "Spock, Lizard?"

Rock, Paper, Scissors, Lizard, Spock is an expansion of Rock, Paper, Scissors created by Sam Kass and Karen Bryla.
It was popularized by The Big Bang Theory TV series.

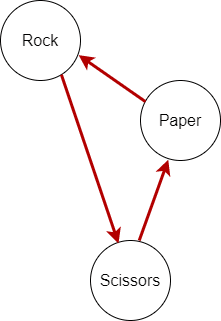
Let's start from the original game:

• Scissors cuts Paper
• Paper covers Rock
• (and as it always has) Rock crushes Scissors

Those traditional Rock, Paper, Scissors rules still apply, but two new options are added to the game: Lizard and Spock.

Let's introduce the simplest rules related to those new options:

• Rock crushes Lizard
• Lizard poisons Spock
• Spock smashes Scissors

No huge surprises for now. Let's add another rule:

• Lizard eats Paper

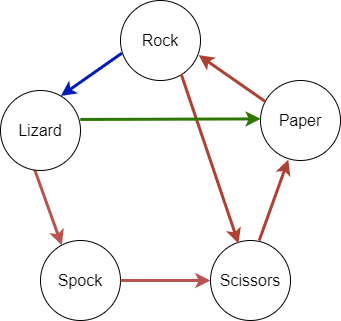
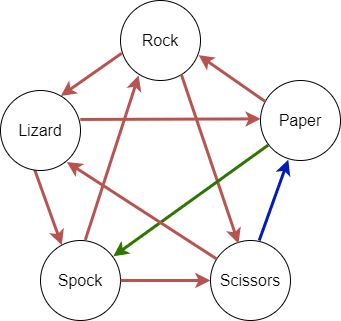
We can already imagine a possible pattern in the arrow diagram, which gets confirmed when adding the next one:

• Spock vaporizes Rock

• Scissors decapitates Lizard

• Paper disproves Spock

After going through all the new rules one by one, we can conclude that there's definitely a pattern.

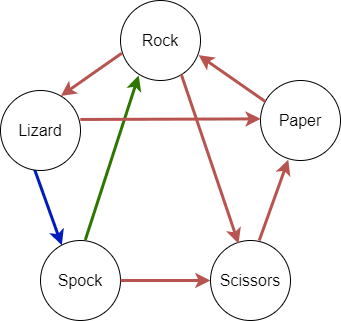
We can also observe such pattern by reflecting those rules in a double entry table, providing we use Rock, Paper, Scissors, Spock, Lizard order (that is, swapping Lizard and Spock positions in the game's name).

Shocking, right? The game's most popular name is Rock, Paper, Scissors, Lizard, Spock, as that's how it appears in The Big Bang Theory; but according to the acronyms used in Sam's page, their creators originally named it 'right' (Rock, Paper, Scissors, Spock, Lizard).

I wonder how Doctor Sheldon Lee Cooper missed that!

Solving the game

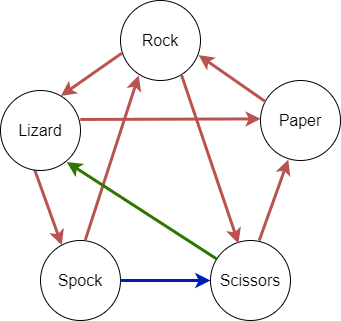
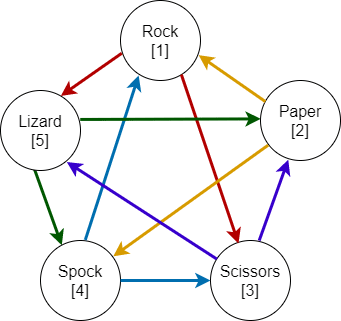
Once all rules are applied, we end up with this final diagram:

Analyzing this figure and/or the table we saw above, we can write the pattern we've identified as:

• Any given option alternates between winning and losing against the other ones if you evaluate it following this (cyclic) order: Rock, Paper, Scissors, Spock, Lizard.
• The sequence starts by either losing against the next option in the list (or the first one clockwise in the diagram) or winning against the previous one (or the first one anti/counterclockwise in the diagram).

That's a really solid start, but still not enough. We need some mathematical relationship to be able to transform that into code.

Let's remember what we concluded for Rock, Paper, Scissors:

• If both numbers are the same, no one wins
• If both numbers are consecutive, the bigger one wins
• If both numbers aren’t consecutive, the smaller one wins

We have to find something similar for our pattern, and that's why we added numbers to the diagram above.

Let's write down some examples and try to induct a general rule that satisfies them all:

• Spock beats Scissors → 4 beats 3 → > number wins
• Spock beats Rock → 4 beats 1 → > number wins
• Paper beats Spock → 2 beats 4 → < number wins
• Lizard beats Spock → 5 beats 4 → > number wins
• Lizard beats Paper → 5 beats 2 → > number wins
• Scissors beats Lizard → 3 beats 5 → < number wins
• Rock beats Lizard → 1 beats 5 → < number wins

By carefully observing the examples, we can induct that:

• If the difference between both numbers is odd, the bigger one wins
• If the difference between both numbers is even:
  • If both numbers are the same, no one wins
  • If both numbers are not the same, the smaller one wins

Feel free to take any other example and verify that it satisfies those statements.

If we implement them using C# 8, we get the following function:

int CalculateWinner(int player1, int player2)
{
    return (Math.Abs(player1 - player2) % 2)
        switch
    {
        0 => player1 == player2
            ? -1
            : new[] { player1, player2 }.Min(),
        1 => new[] { player1, player2 }.Max(),
        _ => throw new Exception(@"¯\_(ツ)_/¯")
    };
}

When we compare it with Rock, Paper, Scissors solution, we see that this algorithm is a generalization of the algorithm we used there, exactly how it's supposed to be, given that we're now solving an expansion of that game.

Console application

Here is an example of an interactive console application that plays Rock, Paper, Scissors, Spock, Lizard with us, and which is based on the previously defined algorithm.

Note that this code can also be used for Rock, Paper, Scissors game if we remove Spock and Lizard from enum Item (line 6).

using System;
using System.Linq;

public static class Program
{
    private enum Item { Rock, Paper, Scissors, Spock, Lizard }

    private static readonly string[] ItemArray = Enum.GetNames(typeof(Item));
    private static readonly Random Rnd = new Random((int)DateTime.Now.Ticks & 0x0000FFFF);

    public static void Main()
    {
        while (true)
        {
            Console.WriteLine($"Let's play! Type '{string.Join("', '", ItemArray[..^1])}' or '{ItemArray.Last()}'");

            if (!Enum.TryParse(typeof(Item), Console.ReadLine().Trim('\''), ignoreCase: true, out var humanInput))
            {
                Console.WriteLine("\tComputer says \"no\": invalid input\n");
                continue;
            }

            var computerInput = Enum.Parse(typeof(Item), ItemArray[Rnd.Next(0, ItemArray.Length)]);
            Console.WriteLine($"\tYou've chosen {humanInput}\n\tComputer has chosen {computerInput}");

            var result = CalculateWinner((int)humanInput, (int)computerInput);

            PrintResultMessage((int)humanInput, result);
        }
    }

    private static int CalculateWinner(int player1, int player2)
    {
        return (Math.Abs(player1 - player2) % 2)
            switch
        {
            0 => player1 == player2
                ? -1
                : new[] { player1, player2 }.Min(),
            1 => new[] { player1, player2 }.Max(),
            _ => throw new Exception(@"¯\_(ツ)_/¯")
        };
    }

    private static void PrintResultMessage(int humanInput, int result)
    {
        var resultMessage = result == -1
            ? "It's a draw!"
            : (result == humanInput) ? "You win!" : "You lose!";

        Console.WriteLine($"\t{resultMessage}\n");
    }
}

You can also find this code here.

I hope you've enjoyed this analysis of Rock, Paper, Scissors, Spock, Lizard and/or that you've found the provided solution interesting!