This is part 2 of a series of my static analyzer for PHP. If you did not read part 1, I suggest you to read it first.

A long time ago, I went to a development user group, and one of the talks was about cyclomatic complexity. At that time, I thought, what a cool name. If you already know the meaning of that cool name. Congrats, you are probably 1 of those developers who can detect lousy code without reading it. By seeing the indentation's shape, you can smell the bad code.

Cyclomatic definition:
Used to describe the number of circuits in a network; equal to the number of edges minus the number of nodes plus the number of graphs.

Ok, breathe. If we translate the definitions into code, it will be something like this.

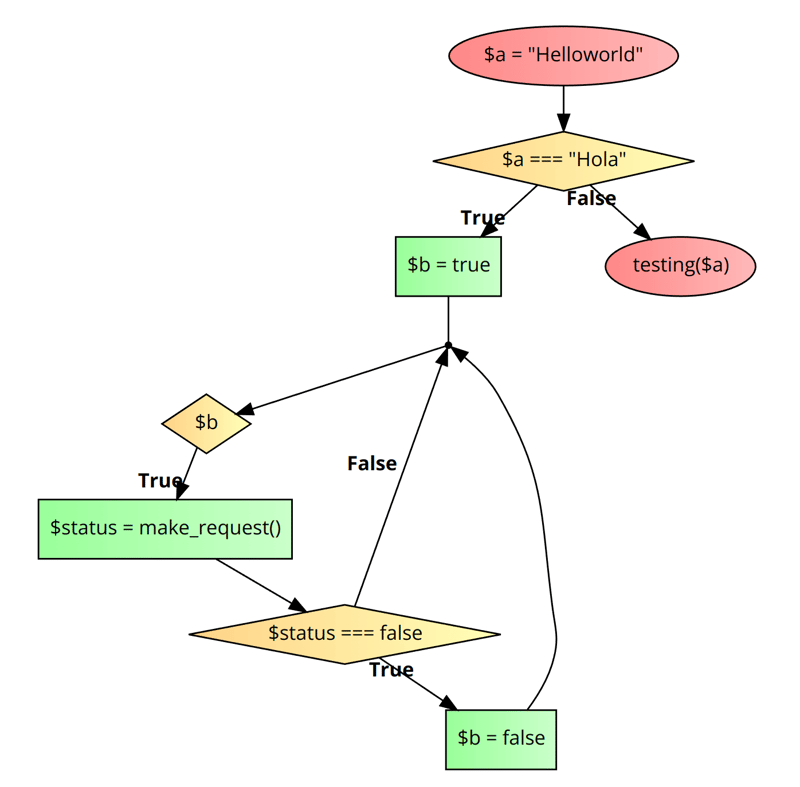
Nodes are like the conditional statement: if, else, while, for, etc.
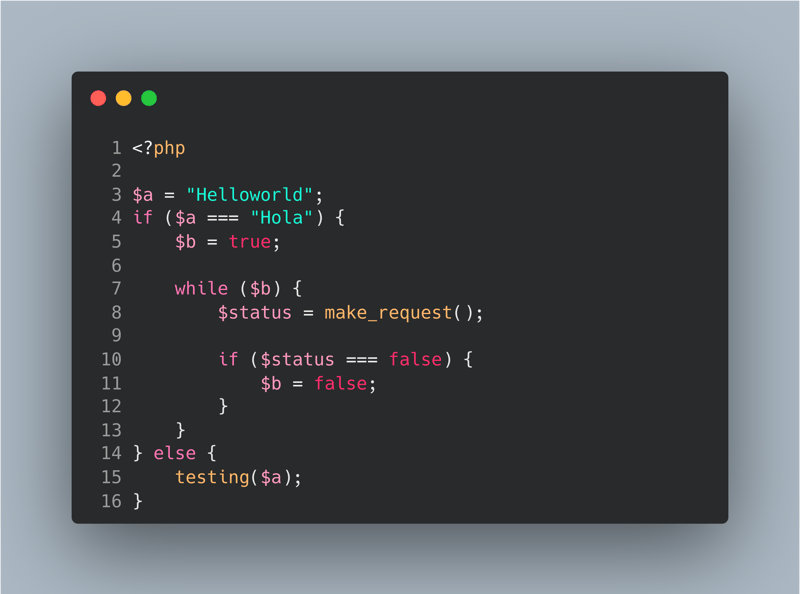
Edges are the paths that can be taken. There are two paths in the code on lines 4 and 14. One of the two can be taken if the variable defined on line 3 has the value of Hola; in this case, the first path will be taken. But in this example, the value of the $a is Helloworld so the second path will be taken. In the control flow graph below, you can view a better representation.

Ok, right; what is the complexity of that cool name I previously told you about?

The code above is a small example, but imagine you have a method that has 100 lines of code. Then, the complexity of the code will increase drastically.

Calculate the complexity

The equation for calculating the cyclomatic complexity is:

This formula is also known as McCabe's Cyclomatic Complexity (MCC) and is widely used to measure the complexity of a program by analyzing its control flow structure.

N stands for the number of nodes, and E stands for the number of edges. The 2P stands for two multiplied by the number of exit nodes. In our example, this will translate into:

So, I started this blog by saying I can prevent myself from writing spaghetti code. If you did not read part 1 of this series, you might not know I'm working on a static analyzer for PHP. The project's name is phanalist, and it's available on github.

In the following paragraph, we will see how phanalist can calculate the cyclomatic complexity of the scope of a method. Before creating Phanalist, I always kept the cyclomatic complexity of the methods I wrote in my mind. And if I see that the complexity is higher than 10. I always try to refactor the method, making it easier to understand.

How does phanalist calculate the cyclomatic complexity? Let's start by implementing the equation above. We will start by creating a struct named Graph. This struct will have the three variables from the equation(n, e, and p).

struct Graph {
    n: i64,
    e: i64,
    p: i64,
}

This struct will be passed around when traversing the abstract syntax tree.

When traversing the AST, we can increase the variables at the right moment. After that, I used the MCC equation to calculate the cyclomatic complexity of our example code.

impl Graph {
    pub fn calculate(self) -> i64 {
        self.n - self.e + (2 * self.p)
    }
}
#[test]
pub fn calculate() {
    let g = Graph { n: 8, e: 9, p: 3 };
    assert_eq!(g.calculate(), 5);
}

In part 1, I explained how to navigate the abstract syntax tree and how Phanalist generates one. If you missed it, I suggest you read that before reading the next part of the series.

In part 3 of this series. I will explain how we traverse the AST when calculating the cyclomatic complexity.