Soo, we're back again with some functional-ish concept. Closures?

I don't know if I haven't said it enough yet, but most of the functional programming concepts are inspired from mathematical concepts, probably that's why they're hard to grasp :"

So what's about this word "closure" and what makes this very concept so special that I talk about?

Well let's first inspect the mathematical concept itself and maybe we can make a projection on typescript/javascript.

In mathematics, a set is closed under an operation if performing that operation on members of the set always produces a member of that set.

Yeah sure.. set? member? totally understandable yeh.

Aight aight, mathematical definitions are always yucky, so let's simplify this one which yields to a common sense.

Let's say that we have the following operation x + y = z and the inputs x and y are of the type integer, take 2 seconds to infer the type of the variable z, surely integer!!

And that is what a closure is in simple words, the set of integers is closed over the operation addition, in other words, any addition between integers will always yield to an integer which within the same set a.k.a Closed Over (Closure)

Alright, what the hell that has to do with typescript?

Well, let's try make a projection from this concept to typescript.

If a closure occurs when an operation is done on a set and returns the same member of this set, which type in typescript/javascript or any other language that can return a type?

Exactly, Functions, they're the only type in most programming languages that can have the return keyword, thus can return a type even if itself.

And surely due to the nature of javascript that functions are first class citizens a function can return another function which makes it a higher order function

that's why Kyle Simpson in his amazing book You don't know JS that closures are only related to functions. I hope that makes sense now.

How can we define a closure in programming?

In order to define closures, we need to have prior knowledge to the lexical scope that exists within javascript environment

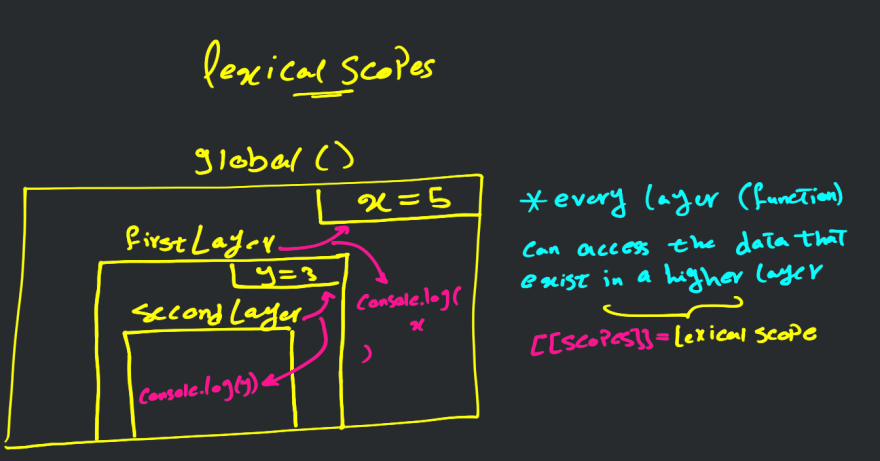
Lexical Scope

Lexical scope is when a group of nested functions have access to their defined variables and the variables that are defined in their parent scope. - Ahmed Osama

I hope that this definition is descriptive enough, but if not, let's inspect it through some code examples.

let x = 5
function firstLayer(): Function {
  console.log(x)

  let y = 3

  return function secondLayer(): void {
    console.log(y)
  }
}

firstLayer()() // logs 5 then 3 to the console

So, where can we inspect the existence of lexical scope?

Well, let's revisit the definition, ... group of nested functions... can be represented as the portion of code where we can return mutliple functions from our firstLayer function

... have access to their defined variables ..., surely all functions can access the functions that are defined in their scope, ... and the variables that are defined in their parent scope that's where the idea of lexical scope exists.

That functions can be thought of as layers or enclosed boxes around some data which are their variables allocated in their local memory. I.E. Execution Context which may be a topic for another article.

Hopefully that ties it down about what is lexical scope.

now let's get back to our main topic.

What is a closure?

Closure is when a function "remembers" its lexical scope even when the function is executed outside that lexical scope. - Kyle Simpson

So what did kyle mean by this definition? Let's inspect via some code snippets.

let x = 5
function firstLayer(): Function {
  console.log(x)

  let y = 3

  return function secondLayer(): void {
    console.log(y)
  }
}

firstLayer()() // logs 5 then 3 to the console

Umm, yeah it's the same code as before, that's because a closure is nothing more than defining some variables in a function and returning a function from this outer function.

These variables are lexically accessible as we discussed earlier. If so, what makes a closure different?

The difference between closure is within the definition "remembers", umm what does mean?

Well, what makes a closure a closure, the ability to re-use these variables defined in firstLayer lexical scope when executed in another lexical scope which is the global scope.

If we inspect the global scope, we wouldn't find any variables called y, but the function firstLayer has one within it's local memory, and it's auto attached to the function secondLayer (closure).

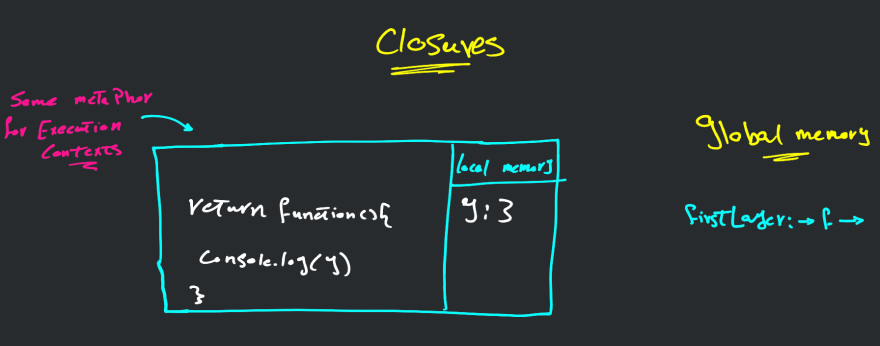
Let's walk through this with some sketching.

so what do we have here?

Well, in global memory we have the reference firstLayer pointing to some object (function) somewhere in the memory heap (We may have another article discussing this too)

and somewhere in our code we executed this function doing firstLayer(), which triggers the function and a variable called y gets stored to the local memory that's allocated by the function.

And the return keyword terminates the execution of the function and returning a function called secondLayer (Name emitted in drawing due to space) which uses the variable y

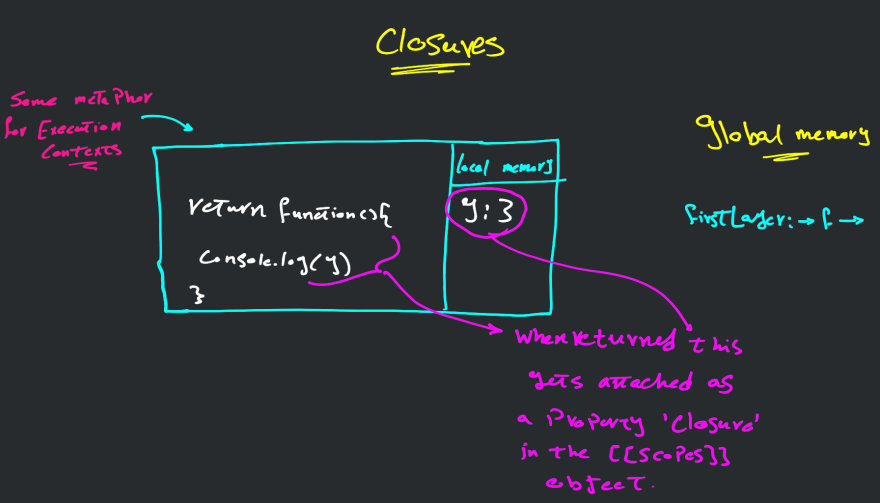
So there might be some confusion, it's known that when a program terminates, all it's allocated memory gets freed.

And our function here is a mini-program, so the allocated memory by it a.k.a the variable y shall be released and deleted from the memory.

How comes that our secondLayer function makes use of it?

The answer is closure

That's what Kyle meant by ...when a function "remembers"...

But, how is this possible? what happens under the hood? Let's see.

Apparently, when the function secondLayer is getting returned from the function firstLayer the compiler makes sure that it has all the variables it may need including the variables that may have been used lexically a.k.a y and attaches them with the function secondLayer under some special property called [[Scopes]] which includes all accessible variables by some function.

let's see some coding example.

const counter = (initial: number = 0) => ({
  decrease: (step: number = 1) => (initial -= step),
  increase: (step: number = 1) => (initial += step),
})

let x = counter()

console.log(x.increase(5)) // 5
console.log(x.increase()) // 6

So you can guess how the compiler though of this code snippet, when the function returned that object, its properties were functions that make use of our local variable initial so, it gets attached aswell to the closure property that exists on the [[scopes]] object.

I hope that wraps it up for what a closure is, now let's get to some use cases.

But I have to say it beforehand, closures are one of the most revolutionary concepts that ever existed in programming. Hope I get you convinced about that too.

Closure use cases

• Partial Applications
• Currying
• Encapsulation
• Trampolines
• Stateful functions
• Mocking classes behavior
• Memoization
• Shaping functions
• Module Pattern
• Generator functions
• Async/Await keyword (yea..)

Phew, exploring how powerful closures are can become overwhelming, imagine that this very simple concept can yield out to all of these great implementations.

Like let's be honest, some of these concepts shape the functional programming paradigm. Guess why, because closures are one of the core pillars of functional programming.

And probably the wierdest one of them all that async/await keywords that were introduced in es2017 (I think) are some application of closures?!

Well, yeah in some sense, surely that's a topic for another article, actually most of these headlines are more like upcoming topics, one of them is already covered in another article you can check it from here Optimizing recursive functions, hopefully I can cover up the rest of these use cases soon.

For now, have a good coffee or some drink and have a very good day ❤️

Appendices and some definitions

First class citizens

First class citizen is when you can pass a value of type x as a parameter to some function y, or assign it to a variable or return it from a function. In another words, if you can treat a function as if it's a string value it's a first class citizen

Higher order functions

Higher order functions are functions that whether accept functions as their inputs or can return functions as their output.

Consider supporting/following me

• Github
• Linkedin
• Youtube
• Website