Conditional Probability and Bayes' Theorem Examples.

Last two weeks I was reviewing statistics fundamentals and had to solve few problems using Bayes' Theorem. Here, I will describe a few techniques I found effective in solving common examples using conditional probability.

When solving these type of problems, I try to solve it ‘intuitively’, if problem is too complicated, then I try to visualize it using probability tree diagram and applying Bayes formula. Finally, if I want to verify my answer, there is an option to do a simulation in Python.

1.Intuitive approach.

So, what is conditional probability? It is a probability of some event ‘A’ given that another event ‘B’ happen. Basically, event ‘B’ gives us some extra information. Let's see the following examples for better understanding.

Example 1A.

A couple has two children. What is the probability that they have two boys?

There are 4 possible combinations for two children: GG, BB, GB, BG. (Where G=Girl, B=Boy). Probability of two boys is P(BB) = 1/4. This is an example of the probability calculation without conditions (or extra information given).

Example 1B.

A couple has two children, one of which is a boy. What is the probability that they have two boys?
Here we have extra information that one of the children is a boy, which narrows possible combinations from 4 to 3: BB, GB, BG.
Probability that two boys given one is a boy P(BB| one is B) = 1/3. This is an example of conditional probability calculation.

Example 1C.

A couple has two children, the older of which is a boy. What is the probability that they have two boys?
Here we have extra information that one of the children is a boy and he is older one, which narrows possible combinations from 4 to 2: BB, BG.
Probability that two boys given older is a boy P(BB| older is B) = 1/2. This is another example of conditional probability calculation.

Example 1D.

The Monty Hall problem is a famous little puzzle from a game show. It goes like this: you are presented with 3 doors. Behind two are goats and behind the third is a car. You are asked to select a door; if you select the door with the car, you win! After selecting, the host then opens one of the remaining two doors, revealing a goat. The host then asks if you would like to switch doors or stick with your original choice. What would you do?
Solution:
There are at least few ways to solve this problem, here I chose the simplest approach.
My initial probability that my choice is correct P(my choice is correct) = 1/3, and probability of that my choice is not correct P(not my choice is correct) = 2/3. But when the host reveals the door with one of the goats, I should switch because probability of ‘not my choice is correct’ is 2/3 and now represented by one door only. And when I switch I will get 'new' probability = 2/3.

2. Construct probability tree diagram.

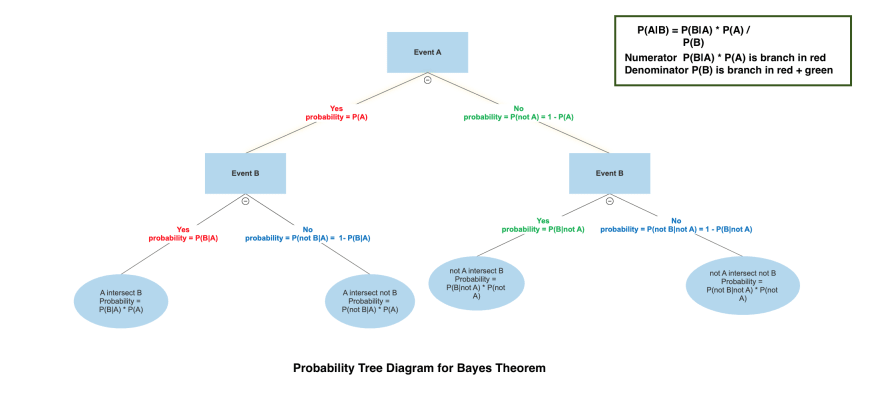
For this method we need to use the Bayes' Theorem Formula:

P(A|B) = P(B|A) * P(A) / P(B)

where
P(A|B) - probability of event A, given event B happen;
P(B|A) - probability of event B, given event A happen;
P(A) - probability of event A;
P(B) - probability of event B;
and P(B) = P(B|A) * P(A) + P(B|not A) * P(not A).

The probability tree diagram could be handy tool when we need to calculate conditional probability, e.g. P(A|B). Probabilities shown in red color are in the numerator in Bayes formula P(B|A) * P(A), denominator P(B) includes probabilities shown in the red and green color P(B|A) * P(A) + P(B|not A) * P(not A).
Let's see that on the examples.

Example 2A.

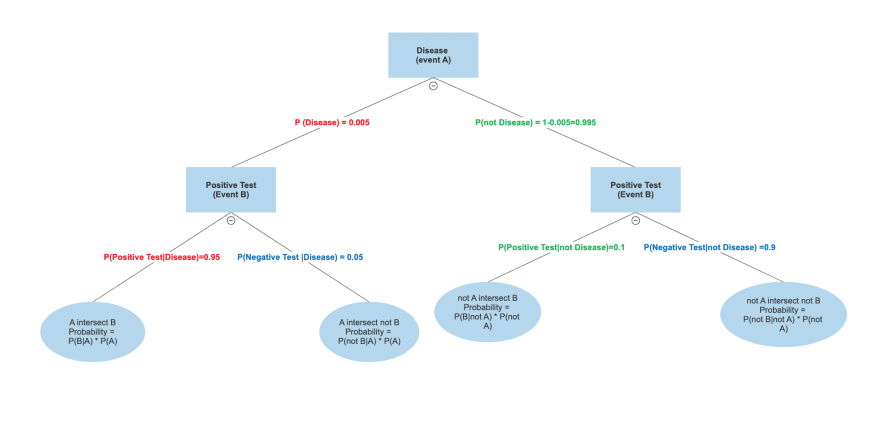
A diagnostic test has a probability 0.95 of giving a positive result when applied to a person suffering from a certain disease, and a probability 0.10 of giving a (false) positive when applied to a non-sufferer. It is estimated that 0.5% of the population are sufferers. Suppose that the test is now administered to a person about whom we have no relevant information relating to the disease (apart from the fact that he/she comes from this population).
Calculate that, given a positive result, the person is a sufferer.
Link to the source.

Solution:
a) construct probability tree

b) We need to find P(Disease|Positive Test).

P(Disease|Positive Test) = P(Positive Test|Disease) * P(Disease) / P(Positive Test).

Numerator is shown in red color:
P(Positive Test|Disease) * P(Disease) = 0.95*0.005 = 0.00475

Denominator is sum of two branches, shown in red and green:
P(Positive Test) = P(Positive Test|Disease) * P(Disease) + P(Positive Test|no Disease) * P(no Disease) = 0.95*0.005 + 0.1*0.995 = 0.10425

Answer is P(Disease|Positive Test) = 0.00475 / 0.10425 = 0.0455

Example 2B.

An aircraft emergency locator transmitter (ELT) is a device designed to transmit a signal in the case of a crash. The Altigauge Manufacturing Company makes 80% of the ELTs, the Bryant Company makes 15% of them, and the Chartair Company makes the other 5%. The ELTs made by Altigauge have a 4% rate of defects, the Bryant ELTs have a 6% rate of defects, and the Chartair ELTs have a 9% rate of defects (which helps to explain why Chartair has the lowest market share).
If a randomly selected ELT is then tested and is found to be defective, find the probability that it was made by the Altigauge Manufacturing Company.
Link to the source.

Solution
a) construct probability tree

b) We need to find P(Altigauge|Defective).
P(Altigauge|Defective) = P(Defective|Altigauge) * P(Altigauge) / P(Defective)

Numerator is shown in red color:
P(Defective|Altigauge) * P(Altigauge) = 0.04*0.8 = 0.032

Denominator is sum of three branches, shown in red, green, and purple color:
P(Defective) = 0.04*0.8 + 0.06*0.15 + 0.09*0.05 = 0.0455

Answer is P(Altigauge|Defective) = 0.032 / 0.0455 = 0.7032

3. Simulation in Python.

Here is the simulation of the Monty Hall problem (Example 1D).

import numpy as np
count_switch = 0 #counter for win when switch
count_stick = 0  #counter for win when stick
for i in range(10000):
    car = np.random.choice([1,2,3])    #assign door 1,2, or 3 to car randomly
    player = np.random.choice([1,2,3]) #assign door 1,2, or 3 to player selection randomly
    if car == player:                  
        # If Initial guess is correct and we stick, increase win numbers for 'stick'
        count_stick += 1 
    else:                              
        # If Initial guess is incorrect and we switch, increase win number for 'switch'
        count_switch += 1 

P_switch = count_switch/(count_switch+count_stick)
P_stick = count_stick/(count_switch+count_stick)

print('Win number when SWITCH:', count_switch)
print('Win probility when SWITCH:', P_switch)
print('Win number when STICK:', count_stick)
print('Win probility when STICK:', P_stick)