Let's build up on our introduction to Trees from last week:

Binary Search

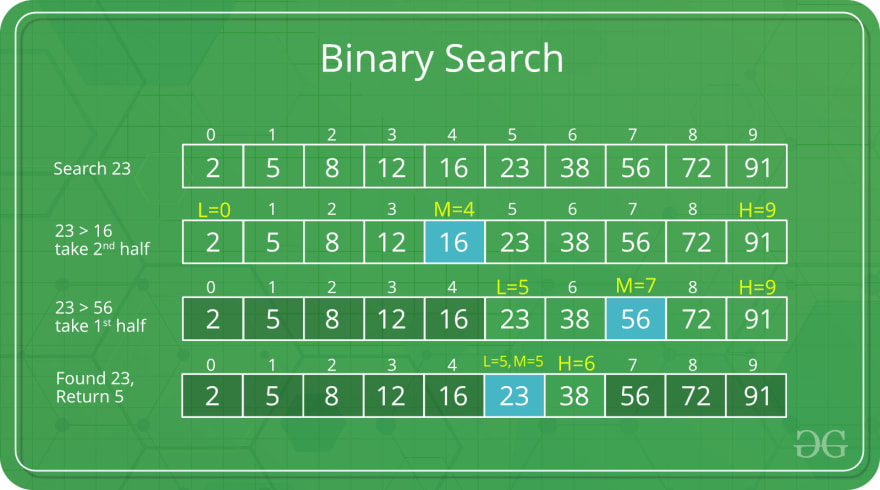
When given a sorted array of data, binary search is a way of searching through that data to find an element in O(log n) time using a divide and conquer approach. It doesn’t require you to look through the entire array in a linear way, which would have a linear big O runtime of O(n).

Binary Search Trees

Binary search trees are a type of tree data structure with the added condition that each element to the left of a node must be less than that parent node, and each element to the right of a node must be greater than that parent node. Each left and right subtree is also itself a binary search tree, which makes searching for elements more efficient.

Learn Binary Search

_{Image credits to geeksforgeeks}

With a sorted data-set, we can take advantage of the ordering to make a sort which is more efficient than going element by element.

Let’s say you were looking up the word “Telescope” in the dictionary. You wouldn’t flip through the “A” words and “B” words, page by page, until you got to the page you wanted because you know “T” is near the end of the alphabet.

You might flip it open near the end and see “R” words. Maybe then you jump ahead and land at “V” words. You would then go slightly backward to find the “T” words.

At each point, you knew to look forward or backward based on the ordering of the alphabet. We can use this intuition for an algorithm called binary search.

Binary search requires a sorted data-set. We then take the following steps:

Check the middle value of the dataset.

If this value matches our target we can return the index.
If the middle value is less than our target

Start at step 1 using the right half of the list.
If the middle value is greater than our target

Start at step 1 using the left half of the list.
We eventually run out of values in the list, or find the target value.

Time Complexity of Binary Search

_{Image credits to freecodecamp}
How efficient is binary search?

In each iteration, we are cutting the list in half. The time complexity is O(log N).

A sorted list of 64 elements will take at most log2(64) = 6 comparisons.

In the worst case:

Comparison 1: We look at the middle of all 64 elements

Comparison 2: If the middle is not equal to our search value, we would look at 32 elements

Comparison 3: If the new middle is not equal to our search value, we would look at 16 elements

Comparison 4: If the new middle is not equal to our search value, we would look at 8 elements

Comparison 5: If the new middle is not equal to our search value, we would look at 4 elements

Comparison 6: If the new middle is not equal to our search value, we would look at 2 elements

When there’s 2 elements, the search value is either one or the other, and thus, there is at most 6 comparisons in a sorted list of size 64.