Logarithms are an elegant mathematical function with a variety of applications from measuring earthquakes to calculating interest rates. But I think they might be under-appreciated as a tool for your average application developer.

The main popular use of logarithms is in charting exponential functions in a way that is intelligible to humans.

You can see this in the bitcoin stock-to-flow price model:

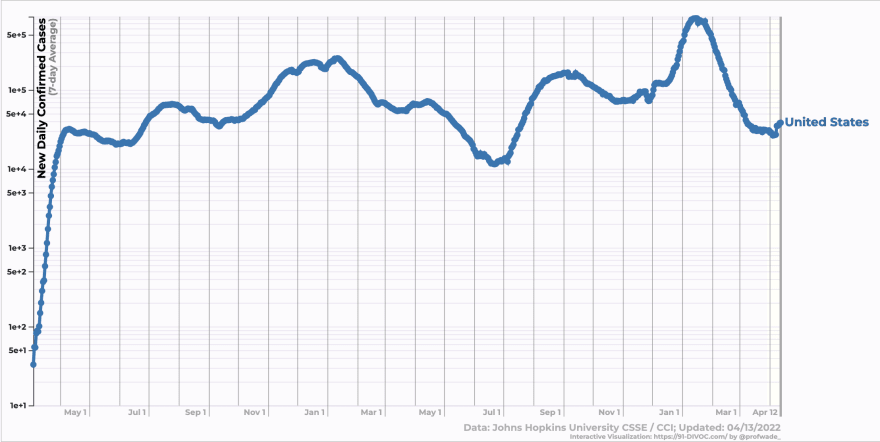
Covid cases:

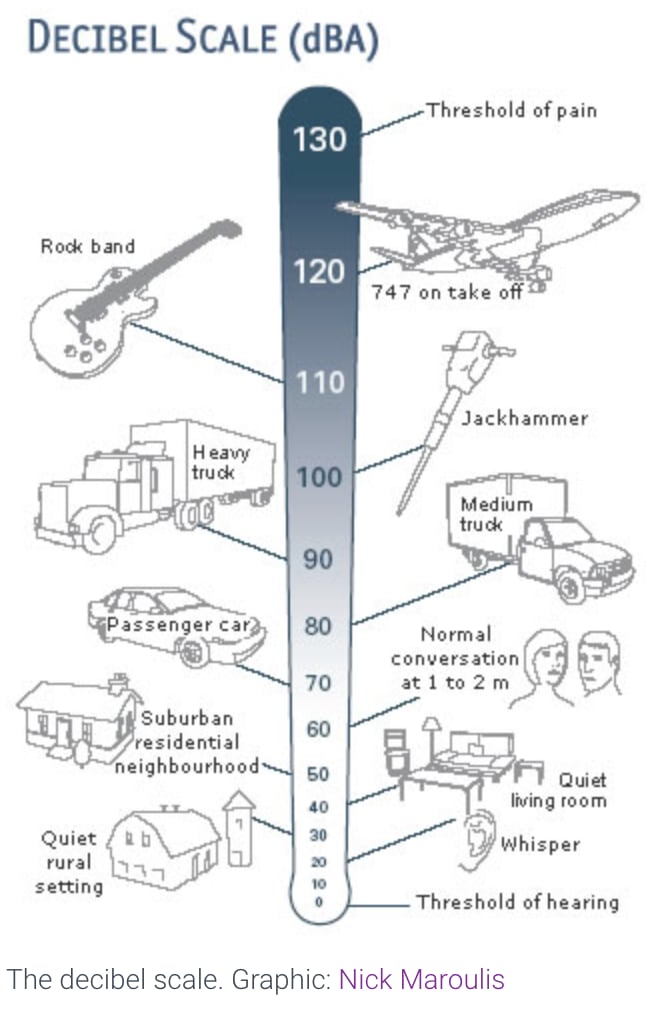
The Decibel scale:

Why not use this powerful tool when relaying everyday concepts to our users?

Here's an example: you might redesign Twitter to show a post's score out of ten rather than the absolute like count, since people with lots of followers have vastly oversized reach compared with nobodies. In other words, there are relatively few high-follower accounts, meaning tweets either get a like or two, or tens of thousands, depending on who you are. What if there was a way to level the playing field a bit?

Let's just say the theoretical maximum number of likes for a tweet is 1 million — anything with 1MM+ likes would have a score of ten. On a linear scale, you would need 1/10th of 1MM likes to score a 1, which obviously won't do.

But we can plot our like numbers on a logarithmic scale using the formula log base likes of max score = exponent. Substituting our max likes and max score into the formula gives us an exponent of 1/6. So, to calculate a given user's score, we just have to raise the number of likes to the power of 1/6, or const getScore = likes => Math.min(10**6, likes) ** (1/6). Here's how that distribution looks

1 like = score of 1
10 likes = score of 1.47
100 likes = score of 2.15
1000 likes = score of 3.16
10000 likes = score of 4.64
100000 likes = score of 6.81
1000000 likes = score of 10

This still feels a little top-heavy to me — let's fine-tune it a bit. One way to do this is to pad lower values with an additional score:

const getScore = likes =>
  (Math.min(10**5, likes) ** (1/5) + Math.min(10**6, likes) ** (1/6)) / 2

This gives us a much nicer distribution:

1 like = score of 1
10 likes = score of 1.53
100 likes = score of 2.33
1000 likes = score of 3.57
10000 likes = score of 5.48
100000 likes = score of 8.41
1000000 likes = score of 10

Applying it to Twitter's UI might turn this:

Into this:

Small change (and not necessarily an improvement), but it illustrates the idea.

Other applications for logarithms in user interface design might include:

• Any other instance where you want to provide an opaque score, especially when incorporating a weighted average of several different data points.
• When you want to weight small values more heavily than large values, for example to give proportionally more voting power to small shareholders in a DAO to reinforce decentralization.

I think this is a very interesting technique, and will be reaching for logarithmic and exponential functions more often in my design work.