Tree and Graph traversal is a popular topic in coding interviews. There are many approaches to graph traversal but one of the most common and important to be familiar with is Depth-First Search (DFS). We'll explore the basic ideas of the algorithm and a few example implementations.

The Basics

Depth-First Search is an algorithm used to traverse graph data structures. It is the order in which the nodes will be visited. As the name implies the traversal is conducted in a depth-first manner, meaning that starting from a certain node we will traverse as deeply into that node as possible before exploring additional nodes. Once a leaf node is found (a node with no children) backtracking will occur until a non-fully explored node is found and the searching will continue in a depth-first manner from there.

Tree Traversal Order

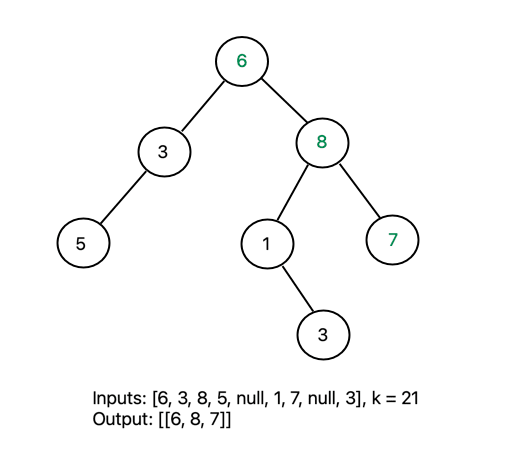
Starting from the root node (6), the left side of the tree is explored to maximum depth before exploring the right. Note that this logic continues from the child nodes as well. From node 8, the left side (8 -> 1 -> 3) is explored prior to the right (8 -> 7).

Non-Tree Traversal Order

DFS can be used with non-tree structures as well. The exploration order may change depending on the starting node and exploration logic, but the concept still holds true. All child nodes are explored to maximum depth before additional nodes are explored.

Implementations

DFS algorithms can be implemented recursively or iteratively using a stack data structure. A recursive implementation utilizes the call stack whereas an iterative solution uses a stack directly. Whilst traversing a graph, nodes are added to the stack and popped off as they are fully explored.

Note: recursive implementations tend to be more common for DFS as they are visually more elegant and straight forward to implement.

Problem

Write an algorithm to check if there are any root to leaf paths where the sum of the path's values equal a given value "k".

class Node {
  constructor(val) {
    this.val = val
    this.left = null
    this.right = null
  }
}

Solution - Recursive

const hasPath = (node, k) => {
  if (node === null) return false

  if (node.left === null && 
      node.right === null && 
      node.val === k) {
        return true
  }
  return hasPath(node.left, k - node.val) || 
         hasPath(node.right, k - node.val)
}

Solution - Iterative

const hasPath = (node, k) => {
  const stack = [ [node, k ] ]

  while (stack.length > 0) {
    const [ node, target ] = stack.pop()

    if (node.left === null && node.right === null && node.val === target) {
      return true
    }

    if (node.right) {
      stack.push([node.right, target - node.val])
    }

    if (node.left) {
      stack.push([node.left, target - node.val])
    }
  }
  return false
}