Striver's SDE Sheet Journey - #12 Count inversions in an array

Problem Statement :-

Given an array of N integers, count the inversion of the array.
An inversion is defined for a pair of integers in the array when the following two conditions are met.

ARR[i] > ARR[j]
i < j

Input : array = [2, 5, 1, 3, 4]

Result : 4

Explanation: We have a total of 4 pairs which satisfy the condition of inversion. (2, 1), (5, 1), (5, 3) and (5, 4).

Solution 1

we can solve this problem by using two nested loop,but it will cost n^2 time complexity.

step-1 initialise a variable pairs=0 .
step-2 run a loop from i=0 to n.

1. run another loop from j=i+1 to n.

check, if arr[i] > arr[j] is true, then increase the inversion count.

step-3 end.

Java

public class Solution {
    public static long getInversions(long arr[], int n) {
        long pairs =0;

     for(int i=0; i<arr.length;i++){

          for(int j=i+1; j<arr.length;j++){

              if(arr[i] > arr[j]) pairs++;
          }
      }
      return pairs;
    }
}

Solution 2

we can also solve this problem by using the Merge Sort algorithm. if you know, how we merge two sorted subarrays in the merge sort algorithm then you can easily understand this solution.

while merging the subarrays, count inversion pairs,
if an element of the left subarray is greater than an element of the right subarray.

let's visually understand how we solve this problem while merging two subarrays.

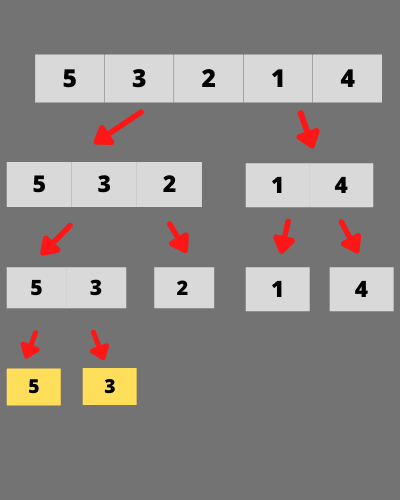
Array = [5,3,2,1,4]

as you can see 5 is greater than 3 which means it satisfies the first condition of inversion pairs and it also satisfies the second one,i<j.
we have found the first inversion pair while merging two subarrays.
pairs - (5,3)

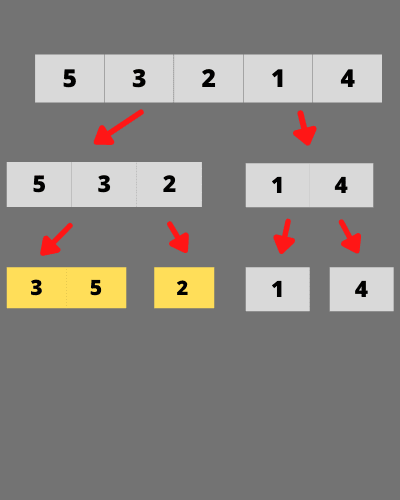
3 > 2 &5 > 2 this pairs also satisfy the both conditions then we will count them as inversion pairs.
pairs - (3,2) (5,2)

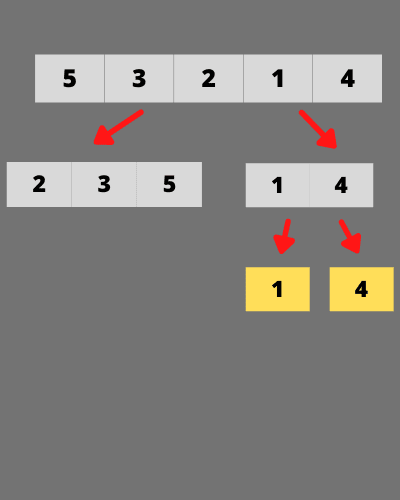
now this time, the left subarray element 1 is not greater than the right subarray element 4, which does not satisfy the first condition of the inversion pairs.

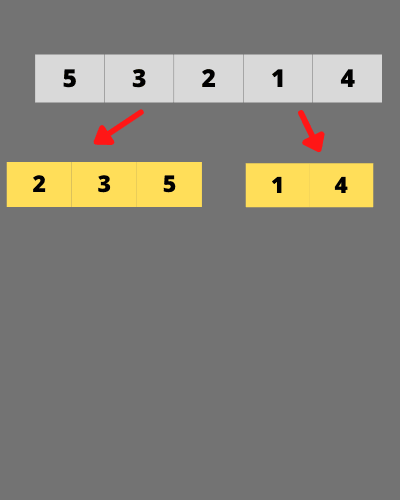
2 > 1 then we can makes - (2,1) (3,1) (5,1) pairs.
2 < 4 doesn't satisfy the conditions.
3 < 4 doesn't satisfy the conditions.
5 > 4 then - (5,4)

Java

public class Solution {
    public static long getInversions(long arr[], int n) {
        // Write your code here.
        long[] ans = new long[1];
        mergeSort(arr,0,arr.length-1,ans);

      return ans[0];
    }

    private static void mergeSort(long[] arr,int left,int right,long[] ans){

    // return if arr size becomes 1
    if(left >= right) return;


    // calculate the mid
    int mid = ( left + right ) / 2;


    mergeSort(arr,left,mid,ans);
    mergeSort(arr,mid+1,right,ans);

    merge(arr,left,mid,right,ans);

   }

     private static void merge(long[] arr,int left,int mid,int right,long[] ans){

    // calculate the size of left & right subarrays
    int leftArrSize = mid - left+1;
    int rightArrSize = right - mid;

    // initialise temp subarrays
    long[] leftArr = new long[leftArrSize];
    long[] rightArr = new long[rightArrSize];

    // copy left & right array into temp arrays
    for (int i = 0; i < leftArrSize; ++i)
      leftArr[i] = arr[left + i];
    for (int j = 0; j < rightArrSize; ++j)
    rightArr[j] = arr[mid + 1 + j];

    // set initial indexes of subarrays
    int leftPointer = 0;
    int rightPointer = 0;
    int arrPointer = left;

    // copy temp subarrays, in ascending order
    while(leftPointer < leftArrSize && rightPointer < rightArrSize ){

      if(leftArr[leftPointer] <= rightArr[rightPointer]){
        arr[arrPointer] = leftArr[leftPointer];
        arrPointer++;
        leftPointer++;
      }else{
        arr[arrPointer] = rightArr[rightPointer];
        arrPointer++;
        rightPointer++;
         ans[0] += leftArrSize - leftPointer; 
      }
    }


    // copy the remaining elements of left subarray into a marge array
    while(leftPointer < leftArrSize){
      arr[arrPointer] = leftArr[leftPointer];
      arrPointer++;
      leftPointer++;
    }

    // copy the remaining elements of right subarray into a merge array
    while(rightPointer < rightArrSize){
      arr[arrPointer] = rightArr[rightPointer];
      arrPointer++;
      rightPointer++;
    }



   }

}

The Time & Space complexity will be the same as the Merge Sort algorithm, O(Nlogn), bcoz we add some lines of code for counting the inversion pairs.

thank you for reading this article, if you find any mistakes, let me know in the comment section and save it for future use.

Blog

Striver's SDE Sheet Journey - #12 Count inversions in an array

sachin26

Solution 1

Java

Solution 2

Java

Join Our Newsletter. No Spam, Only the good stuff.

Related