Graph problems play a pivotal role in various fields, from computer science to logistics. Understanding and solving these problems require a diverse set of algorithms. In this blog post, we'll explore some fundamental graph problems, shedding light on their significance and presenting solutions that cater to different scenarios.

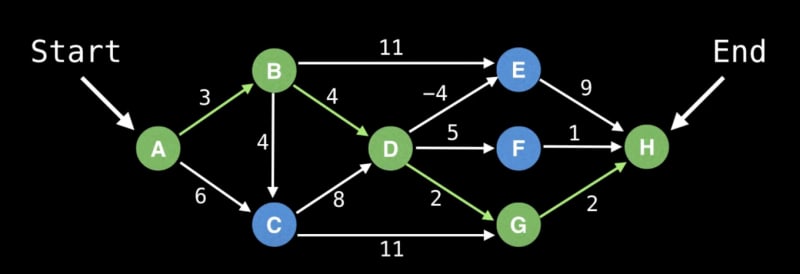
Shortest Path Problem:

The shortest path problem revolves around finding the most efficient route between two nodes in a graph. Various methods can tackle this problem, depending on the nature of the graph:

1. BFS (Unweighted Graph): Ideal for unweighted graphs, BFS systematically explores neighbors to discover the shortest path.

2. Dijkstra's Algorithm: Efficient for graphs with non-negative weights, Dijkstra's algorithm optimally finds the shortest path.

3. Bellman Ford: A versatile algorithm that accommodates graphs with negative weights.

4. Floyd-Warshall: Suitable for all-pairs shortest path problems, handling both positive and negative weights.

5. A*: Combines aspects of Dijkstra's and greedy algorithms, optimizing pathfinding with heuristics.

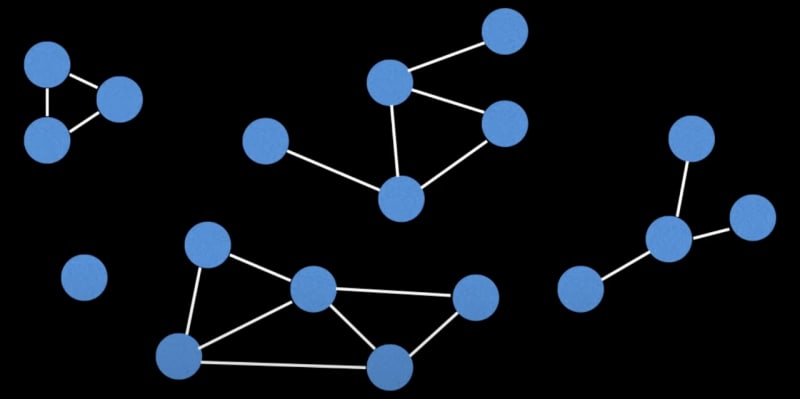
Connectivity:

Determining connectivity involves establishing whether a path exists between two nodes. Here are methods tailored for different scenarios:

1. Union Find Data Structure: Efficiently detects connectivity in disjoint sets.

2. DFS (Depth-First Search): Systematically explores the graph's depth to ascertain connectivity.

3. BFS (Breadth-First Search): Unveils connected nodes layer by layer, aiding in connectivity analysis.

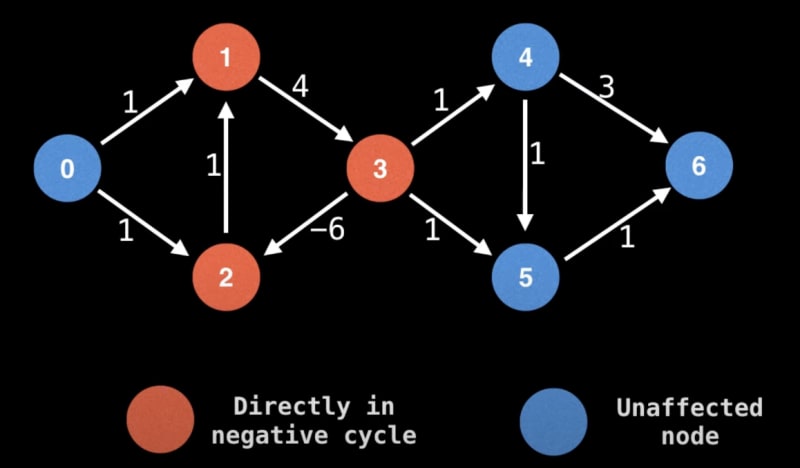
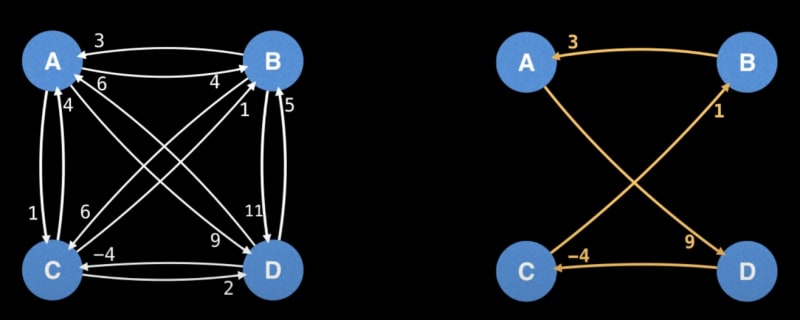
Negative Cycle:

Identifying negative cycles in weighted directed graphs is crucial. The following algorithms are adept at handling this task:

1. Bellman Ford: Detects negative cycles and their locations in the graph.

2. Floyd-Warshall: Extensively applicable, it identifies negative cycles in the graph.

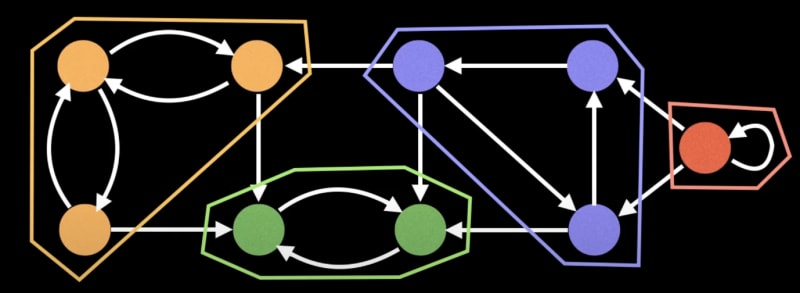
Strongly Connected Components:

Strongly connected components (SCC) are self-contained graph portions in directed graphs. The following algorithms excel in identifying SCC:

1. Tarjan's Algorithm: Effectively identifies SCC in linear time.

2. Kosaraju's Algorithm: Divides the graph into SCC, offering a comprehensive understanding.

Travel Salesman Problem:

The Traveling Salesman Problem (TSP) challenges us to find the shortest path visiting all cities exactly once. As an NP-hard problem, TSP requires sophisticated approaches:

1. Held-Karp with DP (Dynamic Programming): Optimally solves smaller subproblems, building up to the complete solution.

2. Branch and Bound: Systematically explores potential solutions, pruning branches for efficiency.

3. Other Approximation Algorithms like Ant Colony Optimization: Leverages heuristic methods for practical solutions.

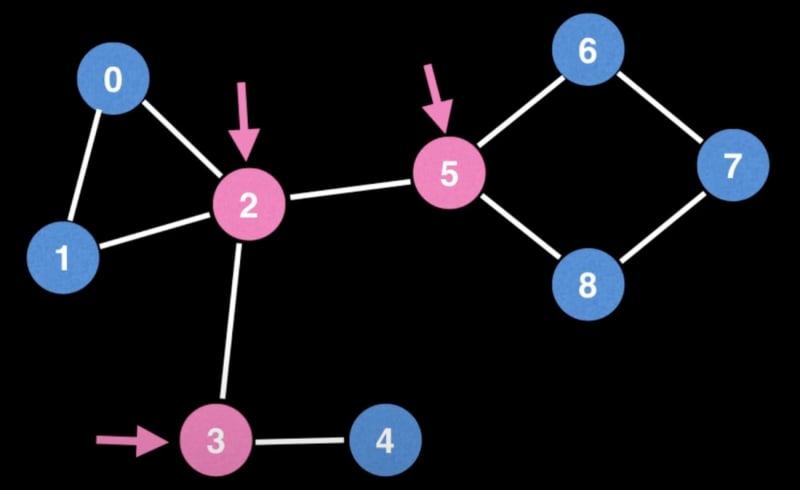
Bridges and Articulation Points:

Bridges and articulation points highlight vulnerabilities in a graph:

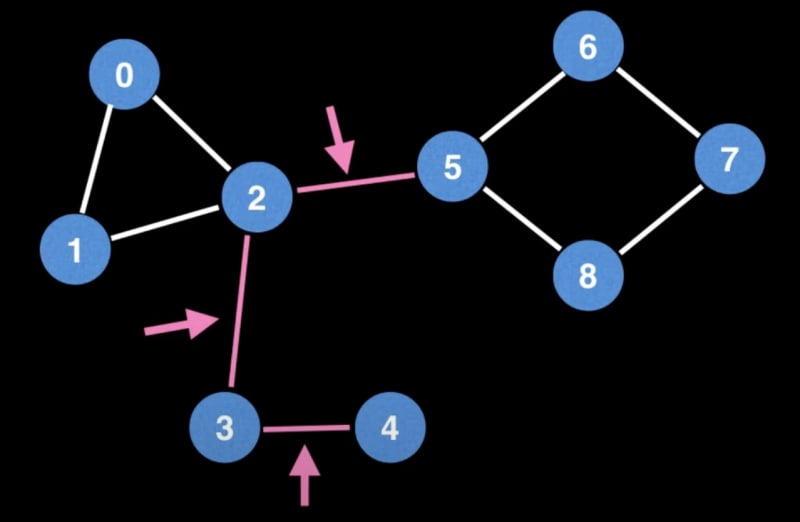
• Bridges: Removing them increases the number of connected components, exposing critical edges.

• Articulation Points: Their removal amplifies the number of connected components, signaling key nodes in the graph's structure.

These indicators often reveal weak points, bottlenecks, or vulnerabilities in a graph.

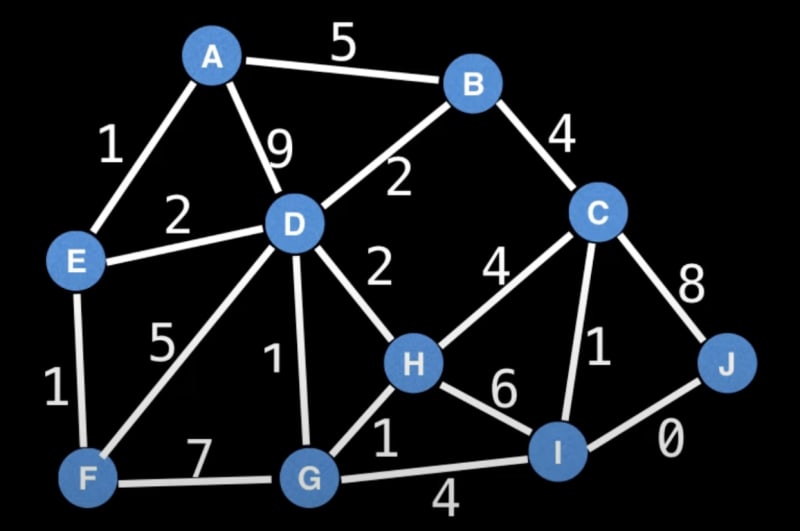
Minimum Spanning Tree:

A Minimum Spanning Tree (MST) connects all vertices with the least total edge weight and no cycles. Algorithms for finding MST include:

1. Kruskal's Algorithm: Greedily selects edges with the smallest weights to construct the MST.

2. Prim's Algorithm: Builds the MST incrementally, selecting the lightest edge at each step.

3. Boruvka's Algorithm: Iteratively adds edges to the MST until all vertices are covered.

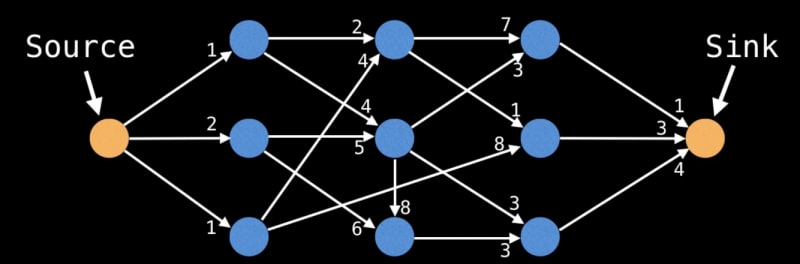
Network Flow (Max Flow):

Determining the maximum flow through a network is crucial in various applications:

1. Ford Fulkerson Algorithm: Augments flow paths to achieve maximum flow.

2. Edmonds-Karp Algorithm: A specialized implementation of Ford Fulkerson using BFS for efficient augmentation.

3. Dinic's Algorithm: Optimizes the augmentation process, enhancing efficiency.

Understanding these graph problems and their solutions equips you with a powerful toolkit for tackling diverse challenges in computer science, optimization, and beyond. Whether you're navigating paths, exploring connectivity, or optimizing flows, these algorithms form the backbone of computational problem-solving.

Connect with me on LinkedIn & X