Neural networks, also known as artificial neural networks (ANNs) or simulated neural networks (SNNs), are a subset of machine learning and are at the heart of deep learning algorithms. Their name and structure are inspired by the human brain, mimicking the way that biological neurons signal to one another.

Neural networks comprise multiple layers and each layer contains a certain number of nodes, each node is connected to each node from previous layer node (except input layer).

The first and the last layer are known as input layer and output layer respectively. Number of nodes in input layer are number of input features which can be represented as a matrix of nxm size where n is number of column and m in number of rows. Output as we can be represented in a matrix.

How ANNs works?

What a neural network do is try to find probability of each node in deep neural network (refer main image) and according to it finding is showing the output.
If you refer to the first image you see, each node is connected to the other node with lines, this line represent an equation.

whole network can be written as

Z → inactivated first layer
W → matrix of weights
A → Data
b → bias

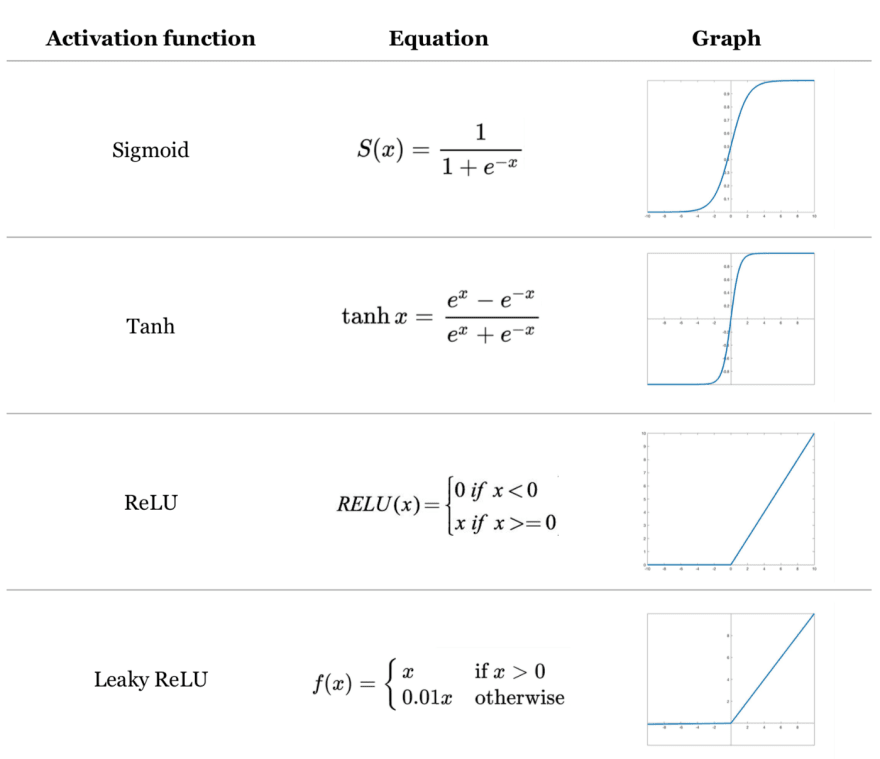
This z function is passed through an activation function which help in understanding complex pattern in ANNs.
If you don't use any activation function in your network, it will only understand linear relationships, which will lead to poor quality ANNs.

On each iteration, 2 values get tuned, i.e., W and b. each iteration comprises two type of prorogation forward and backward propagation

On the first iteration, some random weight and bias will be picked, and an activation function will be applied.
When the propagation finishes, cost function will be calculated which help in tuning of the Weights and biases.

Note:
code use here is from my custom neural network from digit datause here is from my custom neural network from digit data

self.W1 = np.random.rand(10, 784) - 0.5
self.b1 = np.random.rand(10, 1) - 0.5
self.W2 = np.random.rand(10, 10) - 0.5
self.b2 = np.random.rand(10, 1) - 0.5

def forward_propragation(self):
    Z1 = self.W1.dot(self.X) + self.b1
    A1 = self.ReLU(Z1)
    Z2 = self.W2.dot(A1) + self.b2
    A2 = self.softmax(Z2)

Cost function

def backward_propragation(self, Z1, A1, Z2, A2):
    one_hot_Y = self.one_hot()

    dZ2 = A2 - one_hot_Y
    dW2 = 1 / m * dZ2.dot(A1.T)
    db2 = 1 / m * np.sum(dZ2)

    dZ1 = self.W2.T.dot(dZ2) * self.ReLU_deriv(Z1)
    dW1 = 1 / m * dZ1.dot(self.X.T)
    db1 = 1 / m * np.sum(dZ1)

    return dW1, db1, dW2, db2

This function to be low to have a high accuracy. When we have MSE do iterate back which is called a backward propagation.

By doing partial differentiation of the function, you get new weight and biases

to find backward propagation manually

changing the weight and biases

small visualization how a neural net works

in mu custom neural net, I have 1 hidden layer and 10 nodes in it, if you use see the gradient descent function, I am just propagating forward and backward and updating the values

    def gradient_descent(self):
        for i in range(self.iterations):
            Z1, A1, Z2, A2 = self.forward_propragation()
            dW1, db1, dW2, db2 = self.backward_propragation(Z1, A1, Z2, A2)
            W1, b1, W2, b2 = self.update_params(self.W1, self.b1, self.W2, self.b2, dW1, db1, dW2, db2)
            if i % 10 == 0:
                print("ITERATION: ", i)
                print("PREDICTION: ", self.get_predictions(A2))

Full source code : https://github.com/ishubhamsingh2e/neural-network-scratch