How to make money with Java and C++ : IEEE 754 and the real life : 0.1+0.2=0.3 yes, but how?

It's been a while since we've started, it is what it is.

Let's just go straight to the point and see why should we handle money with care.
Here and after Java stands for Java 17 and C++ stands for C++ 20, if not specified differently, I will use w3schools compiler both for Java and C++

The good start in understanding the problem is following the link

C++ : 0.1d + 0.2d != 0.3d

#include <iostream>
#include <limits>
typedef std::numeric_limits< double > dl;

int main() {
  std::cout.precision(dl::max_digits10);
  std::cout<<0.1d<<std::endl;
  std::cout<<0.2d<<std::endl;
  std::cout<<0.3d<<std::endl;
  std::cout<<0.1d + 0.2d<<std::endl;
  std::cout<<(0.1d + 0.2d == 0.3d)<<std::endl;
  return 0;
}

That is clear that following the IEEE 754 the in memory representation is an approximation. Though it's not guaranteed to have always the same approximation as you might have expected.

Java : 0.1d + 0.2d != 0.3d

Let's check for the same in Java :

public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    System.out.println(String.format(DOUBLE_FORMAT, 0.1d));
    System.out.println(String.format(DOUBLE_FORMAT, 0.2d));
    System.out.println(String.format(DOUBLE_FORMAT, 0.3d));
    System.out.println(String.format(DOUBLE_FORMAT, 0.1d + 0.2d));
    System.out.println(0.1d + 0.2d == 0.3d);
  }
}

Thus we can't use double represent money in Java either.

Reduction of summation error

If you are looking to get more consistent results when adding floating point numbers you may check on the Kahan summation algorithm
Otherwise to solve our problem as is we need something simpler, and the name for it is decimal data type support.
In fact we may represent 0.1 as 1 shifted by 1 position to the right, same for 0.2 and 0.3 and then it's simple to add 0.1 and 0.2, we are just summing up 1 and 2 and shift the result to the right. In fact we represent our decimal values as integers with a shift. More details following the link to the decimal 64

Kindly note that when working with decimal types the assignment happens from string to decimal, not from floating point type.

C++ : boost multiprecision 0.1 + 0.2 == 0.3

boost multiprecision

Using the decimal types we get that 0.1 + 0.2 == 0.3

#include <boost/multiprecision/cpp_dec_float.hpp>
#include <iostream>
using boost::multiprecision::cpp_dec_float_50;

int main() {
  cpp_dec_float_50 d01("0.1");
  cpp_dec_float_50 d02("0.2");
  cpp_dec_float_50 d03("0.3");
  std::cout<<std::fixed<<std::setprecision(50)<<d01<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<d02<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<d03<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<(d01 + d02)<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<(d01 + d02 == d03)<<std::endl;
  return 0;
}

Multiplication is straight forward as well

#include <boost/multiprecision/cpp_dec_float.hpp>
#include <iostream>
using boost::multiprecision::cpp_dec_float_50;

int main() {
  cpp_dec_float_50 d01("0.1");
  cpp_dec_float_50 d02("0.2");
  std::cout<<std::fixed<<std::setprecision(50)<<d01 * d02<<std::endl;
  return 0;
}

What about the division ? By default it works the way you would have expected.

#include <boost/multiprecision/cpp_dec_float.hpp>
#include <iostream>
using boost::multiprecision::cpp_dec_float_50;

int main() {
  cpp_dec_float_50 d1("1");
  cpp_dec_float_50 d2("2");
  cpp_dec_float_50 d3("3");
  std::cout<<std::fixed<<std::setprecision(50)<<d1 / d2<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<d1 / d3<<std::endl;
  std::cout<<std::fixed<<std::setprecision(50)<<d2 / d3<<std::endl;
  return 0;
}

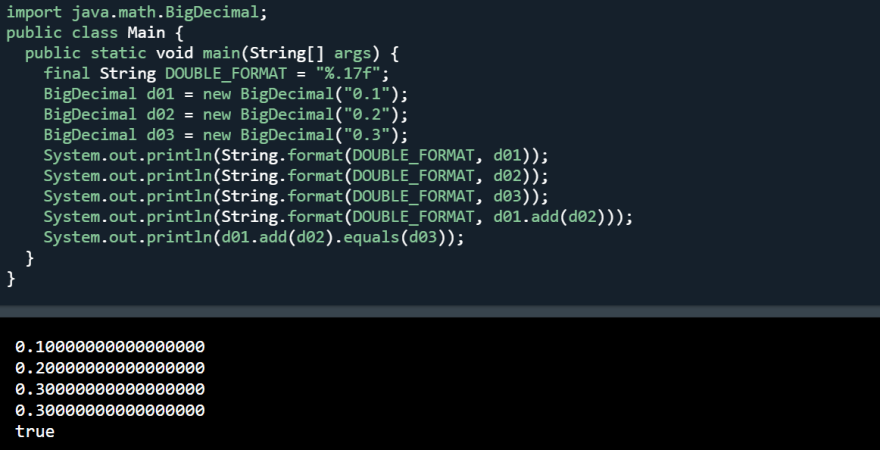
Java : Big Decimal 0.1 + 0.2 == 0.3

Big Decimal

The summation with BigDecimal :

import java.math.BigDecimal;
public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    BigDecimal d01 = new BigDecimal("0.1");
    BigDecimal d02 = new BigDecimal("0.2");
    BigDecimal d03 = new BigDecimal("0.3");
    System.out.println(String.format(DOUBLE_FORMAT, d01));
    System.out.println(String.format(DOUBLE_FORMAT, d02));
    System.out.println(String.format(DOUBLE_FORMAT, d03));
    System.out.println(String.format(DOUBLE_FORMAT, d01.add(d02)));
    System.out.println(d01.add(d02).equals(d03));
  }
}

and the multiplication :

import java.math.BigDecimal;
public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    BigDecimal d01 = new BigDecimal("0.1");
    BigDecimal d02 = new BigDecimal("0.2");
    System.out.println(String.format(DOUBLE_FORMAT, d01.multiply(d02)));
  }
}

work as you might have expected, for the division there is a particularity, either a result of division must be representable in a finite decimal way or we need to pass a MathContext

import java.math.BigDecimal;
public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    BigDecimal d1 = new BigDecimal("1");
    BigDecimal d2 = new BigDecimal("2");
    BigDecimal d3 = new BigDecimal("3");
    System.out.println(String.format(DOUBLE_FORMAT, d1.divide(d2)));
  }
}

import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    BigDecimal d1 = new BigDecimal("1");
    BigDecimal d2 = new BigDecimal("2");
    BigDecimal d3 = new BigDecimal("3");
    System.out.println(d1.divide(d3, MathContext.DECIMAL32));
    System.out.println(d1.divide(d3, MathContext.DECIMAL64));
    System.out.println(d1.divide(d3, MathContext.DECIMAL128));
    System.out.println(d1.divide(d3, 2, RoundingMode.HALF_EVEN));

  }
}

import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
public class Main {
  public static void main(String[] args) {
    final String DOUBLE_FORMAT = "%.17f";
    BigDecimal d1 = new BigDecimal("1");
    BigDecimal d2 = new BigDecimal("2");
    BigDecimal d3 = new BigDecimal("3");
    System.out.println(d2.divide(d3, MathContext.DECIMAL32));
    System.out.println(d2.divide(d3, MathContext.DECIMAL64));
    System.out.println(d2.divide(d3, MathContext.DECIMAL128));
    System.out.println(d2.divide(d3, 2, RoundingMode.HALF_EVEN));

  }
}

Summary

Whenever you are working with money it's a good idea to use either integer or decimal type. It may happen that you need to write a custom decimal type for your needs, in this case the general guidelines could be the following :

constructor from a string (or a factory)
internal representation as an integer with a shift (also integer)
handling of rounding during division

And therefore it could be even better a idea to consider a use of a provided decimal type or a lib.
Take care.

Blog