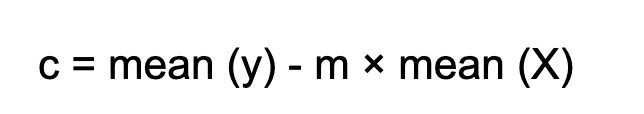The basis of many machine learning models used to make predictions today is statistics, from statistical analysis brings forth their implementation in the form of algorithms. In this article, we will look into one of sklearn’s supervised machine learning linear algorithms for predicting regression values, Linear Regression.

Understanding Linear Regression

Linear regression is based on the concept:

Y=C+M*X

Where C is the intercept of the plotted graph, it determines where the line touches the y-axis, Y is the target or predicted value and X represents the features, sometimes in the dataset X may vary in the sense that there may be more than one feature. Which leads to an equation.

Y=C+M1*X1+M2*X2….+Mn*Xn

The C and M are regarded as the bias in Machine Learning because it is added to the offset of all predictions that will be made.

To get the values of M.

Where Xi are the different input values of X used to predict Y. and Mean are the average values of the number of X inputs.

And to derive the value of the intercept c.

Creating the Model from Scratch

So we now have a brief review of how the model works, now to implement it.
We start by importing the numpy library as we would make use of it for some numerical calculations. We create the class LinearRegression and set some initialized parameters.

import numpy as np
class LinearRegression:
    def __init__(self, fit_intercept=True):
        self.fit_intercept = fit_intercept
        self.coef_ = None
        self.intercept_ = None

The class takes in the fit_intercept parameter which determines whether an intercept term would be included in the model. Its default value would be true. The coefficients and the intercept would be set as none for default values which would later be changed when the model is trained with data.

def _add_intercept(self, X):
        return np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)

Next, we create a function ‘_add_intercept’ so that the model takes in the values of X and It creates an array of ones with the shape (X.shape[0], 1), representing the intercept term, and concatenates it with X along the y-axis.

 def fit(self, X, y):
        if self.fit_intercept:
            X = self._add_intercept(X)
        self.coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
        if self.fit_intercept:
            self.intercept_ = self.coef_[0]
            self.coef_ = self.coef_[1:]

Next, we create a function in the class that fits the data into the model and performs some algorithmic calculations. It uses a closed-form solution that involves the use of matrix operations. It first takes the parameters X and Y and if fit_intercept is set to True it passes X through the _add_intercept function to add an intercept term. Next is the algorithm to compute the values of the coefficients by getting the inverse of the dot products of X and the dot product of the transpose of X and get the dot product of those with y. Then if the fit_intercept function is True, it takes the first value in self.coef as the intercept, and the rest are the coefficients.

def predict(self, X):
        if self.fit_intercept:
            X = self._add_intercept(X)
        return X.dot(np.concatenate(([self.intercept_], self.coef_)))

Next, we create predict function which takes in the value of X and if ‘fit_intercept’ is true it passes the values of X into the _add_intercept function and returns the dot product of X and the concatenated array of the intercept and coefficients.

Here’s the full code below:

import numpy as np
 class LinearRegression:
    def __init__(self, fit_intercept=True):
        self.fit_intercept = fit_intercept
        self.coef_ = None
        self.intercept_ = None
    def _add_intercept(self, X):
        return np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)
    def fit(self, X, y):
        if self.fit_intercept:
            X = self._add_intercept(X)
        self.coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
        if self.fit_intercept:
            self.intercept_ = self.coef_[0]
            self.coef_ = self.coef_[1:]
    def predict(self, X):
        if self.fit_intercept:
            X = self._add_intercept(X)
        return X.dot(np.concatenate(([self.intercept_], self.coef_))) 

Thanks for reading. Like, and comment your thoughts below.