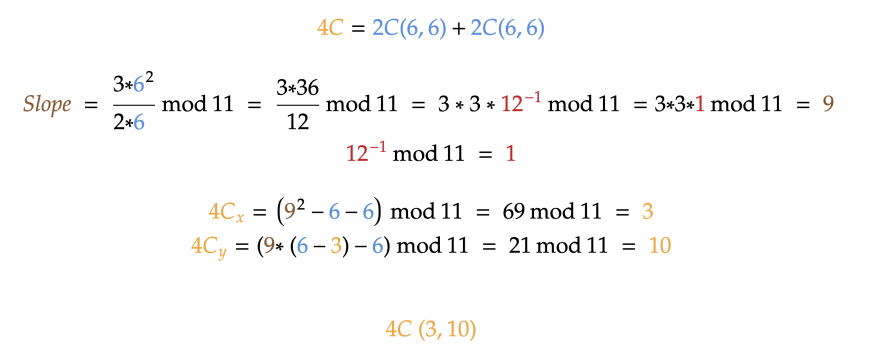The series consists of four parts; each part uses the concepts discovered in the previous parts:

1. The Magic of Elliptic Curves
2. The Magic of Elliptic Curves Combined with Finite Fields [you’re here]
3. Using The Magic of Elliptic Curves to Sign and Verify Messages
4. ECDSA Implementation in Python Using Zero Dependencies

The Essentials of Finite Fields

We don’t need to study everything about finite fields. All we need here is to understand a couple of essential properties to move on and be able to operate on a certain “algebra” of finite fields.

To simplify, finite field is an algebraic concept where we have a finite number of elements, which we can add, subtract, multiply, or divide, and the algebra will continue working properly.

Have you heard of the modulus operation? If you’re a programmer, probably you did. This is just a reminder of division, and in programming languages, it’s usually expressed as a % (or mod) operator. For example:

2 mod 11 = 2
10 mod 11 = 10
11 mod 11 = 0
13 mod 11 = 2
14 mod 11 = 3

If we try numbers from 0 to 33 mod 11, we will get these numbers:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0

It works like a clock. We can call this a finite field of order 11.

We need to know just 4 properties:

• The order of multiplication doesn’t matter.
  a*b*c mod n is the same as (a mod n) * (b mod n) * (c mod n) mod n, which is the same as (a*b mod n) * c mod n
  Example:
  6 * 7 * 8 mod 11 = 336 mod 11 = 6, same as:
  (6 * 7 mod 11) * 8 mod 11 = (42 mod 11) * 9 mod 11 = 9 * 8 mod 11 = 72 mod 11 = 6

• Negative number mod n is the same as n-(|negative number| mod n).
  Examples:
  -4 mod 11 = 11-(4 mod 11) = 11-4 = 7
  -7 mod 11 = 11 - (7 mod 11) = 11 - 7 = 4
  -9 mod 11 = 11 - (9 mod 11) = 11-9 = 2
  -2 mod 11 = 11 - (2 mod 11) = 11 - 2 = 9
  -13 mod 11 = 11 - (13 mod 11) = 11 - 2 = 9

• “Multiplicative inverse”: for any a, there is a number b, such as a*b mod n = 1.
  If a * b mod 11 = 1, a is called the multiplicative inverse of b modulo n, and vice versa: b is called the multiplicative inverse of a modulo n.
  Example:
  1) 5 * x mod 11 = 1. Let’s try values for x one by one, and we will find out x = 9. So 9 is the multiplicative inverse of 5 modulo 11.
  2) 7 * x mod 11 = 1. Let’s try our brute force again and we will find out x = 8. 8 is the multiplicative inverse of 7 modulo 11.
  3) 10 * x mod 11 = 1. x = 10. So 10 is the multiplicative inverse of 10 modulo 11.
  Usually, it’s done by the extended Euclidean algorithm, but it’s a matter of a separate article. So for now, let’s just use brute force.
  Also, n must be a prime number!

• The division is the same operation as multiplication by the multiplicative inverse! Last and the most important property:

So, when we need to deal with division mod n, we can easily calculate it.

Let’s see an example:

Why is 2 the multiplicative inverse of 6 mod 11? Because 6 * 2 = 12, 12 mod 11 = 1.

That’s it! Now we know how to operate on finite fields “algebra”.

Elliptic Curves Over Finite Fields

Here’s where it becomes less obvious and a little harder to understand. But this is exactly how elliptic curves are used in cryptography. What we need to do is exactly what is said in the title: "put our elliptic curve over a finite field."

So, here is how our formula changes:

Everything is the same as in the original formula but now both parts of the equation are now under the modulo p.

Let’s use the elliptic curve with the following configuration for our examples:

• a = 0
• b = 7
• p = 11

Let’s find all the points on this curve running this code:

const a = 0;
const b = 7;
const p = 11; 

for (let x = 0; x <= p; x ++) {
  for (let y = 0; y <= p; y ++) {
    if (y**2 % p === (x**3 + a * x + b) % p) {
      console.log(`(${x}, ${y})`);
    }
  }
}

Here is the result:

(2, 2), (2, 9), (3, 1), (3, 10), (4, 4), (4, 7), (5, 0), (5,11), (6, 5), (6, 6), (7, 3), (7, 8)

Let’s see what it looks like on a coordinate grid:

Let’s try a=0, b=7, p=23:

Doesn’t look like anything, right? No distinguishable shape.

But! What turns out is that it preserves all the properties and formulas of the “original” elliptic curve!

So now we’ve got an elliptic curve, that doesn’t look like an elliptic curve. But! It has a finite set of points, and most importantly, works like an elliptic curve.

We need to slightly modify our formulas from PART I with respect to mod p:

• Multiplying a point by -1:
  If we have a point A(x, y), we can easily get -A by multiplying its y coordinate by -1 modulo p.
  Example:
  -1 * A(2, 2) → -A(2, -2 mod 11) = -A(2, 9)
  -1 * A(2, 9) → -A(2, -9 mod 11) = -A(2, 2)
  -1 * A(6, 5) → -A(6, -5 mod 11) = -A(6, 6)
  -1 * A(6, 6) → -A(6, -6 mod 11) = -A(6, 5)

• Adding two points together:

• Adding a point to itself:

If you don’t yet understand the concept of multiplicative inverse, please, go back to PART II and check it once more.

That’s it! Time to practice!

For our examples, we will use the elliptic curve with a=0, b=7, and order p=11.

Let’s pick a point C(7, 8) and calculate 2C:

We can now easily calculate 4C:

Now let’s calculate 4C - C, which is essentially 3C = 4C + (-C):

Now let’s add 3C = C + 2C and see if the result is the same:

The math perfectly works here!

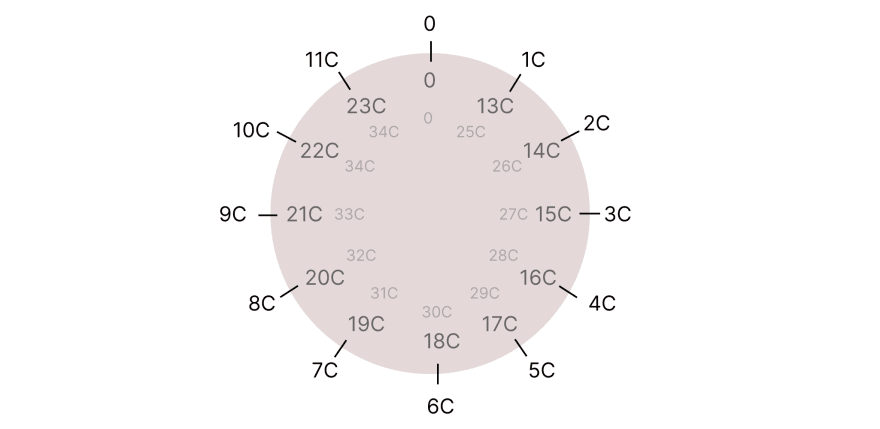
One super important property: Every point on a curve has its own order n!
It works like a modulo. For example, if the order n of point C is 12, it means that 12*C = 0(the point doesn’t exist), 13*C = C, 16*C = 4C, 27*C = 3C. This property is predefined for a point.

You can practice and make sure it works.

The order of our point C is actually 12. I suggest a task for you: try calculating 8C by adding 4C + 4C. Then try adding 8C + 8C. You will get 16C, which will be the same point as 4C.

It works like a clock:

Now we know absolutely everything essential for using the elliptic curves in cryptography.

To recap

• All formulas work fine. We can still calculate any integer x * Point. We still need approximately log2(x) operations!
• Elliptic curves have now a finite set of points
• Points now have their own order n, so they tend to repeat themselves like in a clock.
• To define an elliptic curve, we now need three variables: a, b, and p. p is called the order of an elliptic curve.

How do we know, which a, b, and p to use? It’s standardized! There are many standards out there.

What do Bitcoin and Ethereum use?

They use the standardized elliptic curve called secp256k1. It has the following variables:

• a=0
• b=7
• p=115792089237316195423570985008687907853269984665640564039457584007908834671663

Quite a big number! I think you’re starting to guess why elliptic curves are so good for cryptography.

Now that we know everything essential, let’s use it in cryptography in the next part!

Next part: Using The Magic of Elliptic Curves to Sign and Verify Messages

Feel free to contact me and ask questions:

exemak@gmail.com
t.me/exemak
Mikhail Karavaev