Ao longo da minha leitura do Entendendo Algoritmos, eu tenho revisitado muitos conceitos e técnicas que eu já havia me esquecido que existiam e algumas que eu nunca consegui entender (até agora haha). Dentro desse post (e em mais alguns outros q vão vir ao longo da minha leitura) eu vou trazer esses conceitos sob uma análise de estudos pessoais.

O que é 'Recursão'?

Imagine que você chegou na academia e tava tão empolgado com o treino que colocou sua carteira no primeiro armário vazio que você achou. Quando acabou o treino, você não consegue mais lembrar em qual armário você guardou suas coisas então, vai abrindo um de cada vez até você encontrar.

Recursão começa por aí, executar uma função de forma repetida até encontrar o resultado correto.

Mas... isso também não seria um loop?

Sim, um loop pode ser uma alternativa para resolver tipos de situações como essa. Inclusive, há casos em que loops são mais benéficos pois, recursão não trás nenhum bônus em termos de desempenho.

E por mais não-atrativo que eu esteja fazendo recursão parecer, ela tem uma qualidade sem igual: Objetividade.

Mas, resumindo:

Recursão é quando uma função chama a si mesma.

Como estruturar uma recursão?

Ao estruturar uma recursão, temos duas sub-estruturas:

- Caso recursivo: Quando a função chama ela mesma.

Ex: Abrir um armário de cada vez, de forma contínua.

- Caso-base: Quando a função não chama ela mesma, evitando um loop infinito.

Ex: Parar de abrir os armários quando encontrar a carteira.

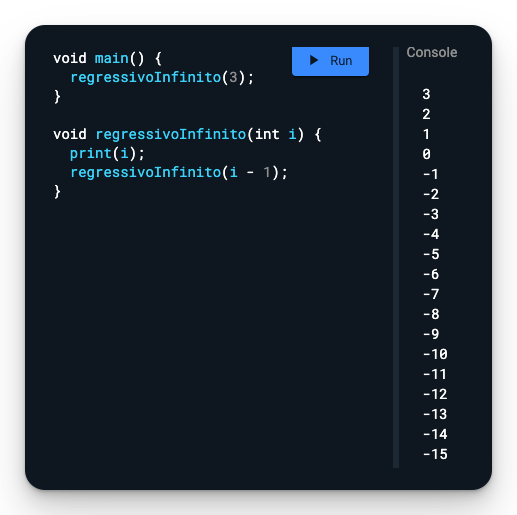
Como assim um loop infinito? Pse, quando mal implementado, pode acontecer de uma função recursiva ficar chamando ela de novo e de novo para sempre. E como não queremos isso, vamos entender como estruturar uma.

Esse é um exemplo de loop infinito. Presta atenção em como os números continuam reduzindo para sempre.

#MinhaPrimeiraRecursão

Vamos exemplificar recursão ao calcular o fatorial (!) de um número (num).

num = 3, portanto 3! = 3 x 2 x 1 => 6.

Problema: Descobrir o fatorial de um número.

Solução: Multiplicar esse número por: ele mesmo - 1, até ele ser igual a 1.

• Caso recursivo: Multiplicar esse número por: ele mesmo - 1.

• Caso-base: até ele ser igual a 1.

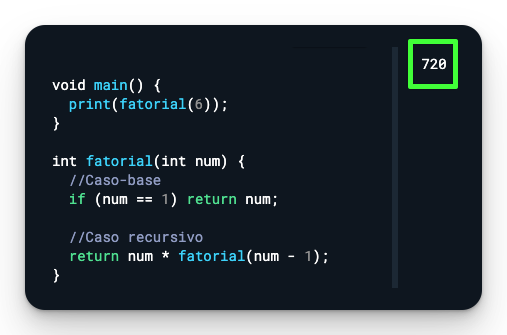
Isso em código fica assim:

Pilha e o lado sombrio da recursão

Recursão é estruturada em cima de pilhas, assim como muitas coisas no seu computador. E, o que é uma pilha?

Pilha é uma estrutura de dados onde o último dado inserido, é o primeiro a sair. Por exemplo, você tem uma pilha de livros para ler, quando for iniciar a leitura, você pega o livro que está no topo, e assim sucessivamente até a pilha não existir mais. Para entender mais sobre pilhas, aqui tem um material massa!

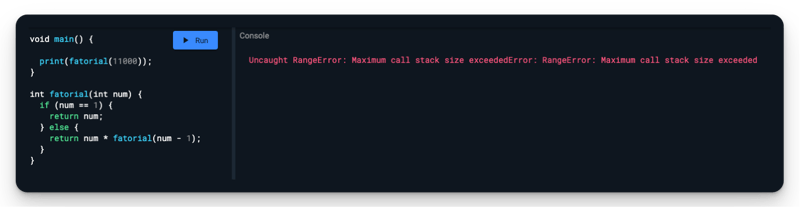
Contudo, ainda que recursão traga a magia da Objetividade tem a desvantagem de que você pode acabar sobrecarregando a sua pilha (da uma olhada nesse artigo para entender porque isso acontece), como no exemplo abaixo:

Mas, não precisa temer. Tem sempre outras duas alternativas:

• Voltar para o bom e velho loop;
• Utilizar Recursão de Cauda.

Recursão de Cauda

Se você utiliza dart, já vou deixar adiantado que isso não vai dar certo e aqui e aqui também vão ter descritivos melhores das informações referentes à isso.

Mas, caso você utilize uma linguagem que tenha suporte para Recursão de Cauda, ou curiosidade em como funciona, vamos aos trabalhos.

O que diferencia a recursão de cauda da recursão normal é que a primeira utiliza menos memória durante o processo de empilhamento, fazendo com que ela seja mais rápida.

Comparando de forma prática, ao calcular 5!, que é igual a 120, vemos uma diferença importante entre a recursão simples e a recursão de cauda. Na recursão comum, são necessárias 120 variáveis para rastrear as chamadas. Porém, na recursão de cauda, isso não é preciso, uma vez que a chamada recursiva é a última operação executada pela função. Isso simplifica o processo e economiza recursos, tornando o código mais eficiente.

E ainda que dart não tenha a otimização de recursão em cauda, ainda sim temos o exemplo abaixo de como ela seria estruturada.

Resumão

• Recursão é quando uma função chama a si mesma;
• Recursão é uma boa alternativa para loops quando você está buscando mais objetividade;
• Às vezes pode acontecer de sua pilha ficar muito grande quando utilizar recursão;
• Você pode contornar o problema da pilha grande com loops ou com recursão de cauda.

Referências

Notas de Aula – Algoritmos e Programação de Computadores
Recursão de cauda para iniciantes