A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child.

Boundary Traversal Binary Tree is a common programming problem. You will be given a binary tree, and you have to print the boundary nodes of the binary tree in an Anti-Clockwise fashion starting from the root.

The boundary traversal of binary tree includes the left Boundary, leaves, and right Boundary without duplicate nodes but the values of nodes may contain duplicates.
There are mainly two types of Boundary, i.e., the left Boundary and the right Boundary. The left Boundary is the path from the root to the leftmost node, whereas the right Boundary is the path from the root to the rightmost node. If the root node does not contain any left and right subtree, then the root node itself would be considered the left Boundary or the right Boundary.

Note: This definition only applies to the input binary tree, not any subtrees.

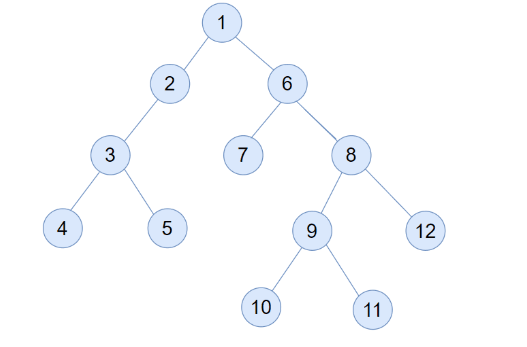
Consider this Binary Tree

The leftmost node is a leaf node that can be reached by first traveling to the left subtree if one exists. If not, go to the right subtree. Keep going down until you reach a leaf node. Left Boundary is shown using red nodes in the given Binary Tree.

The rightmost node is a leaf node that can be reached by first traveling to the right subtree if one exists. If not, go to the left subtree. Keep going down until you reach a leaf node. Right Boundary is shown by red nodes in the below given binary tree.

Leaves of the above binary tree are shown using red color.

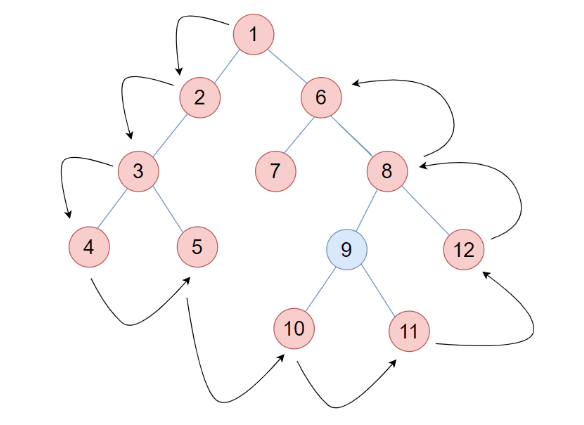
Therefore, boundary traversal of the above Binary tree is

1 -> 2 -> 3 -> 4 -> 5 ->7 -> 10 -> 11 -> 12 -> 8 -> 6

Algorithm
The idea is to divide this problem into four sections:

1. First, print the root node.
2. Print the left boundary from the top down.
3. In the same sequence as the inorder traverse, print the leaf nodes.
4. Print the right boundary from the bottom up.

This approach seems simple, but there are a few edge cases that need to be taken care of in order to prevent duplicates:

• The root node is printed by both the left and right boundary traversals. We can avoid this repetition by printing the root node first, then traversing the left Boundary on the root's left child and the right Boundary on the root's right child.

• Leaf nodes are the binary tree's leftmost and rightmost nodes. They will be printed during the traversal of the left and right boundaries when printing the leaf nodes. To avoid this, when traversing the left and right boundaries, leave out the leaf nodes.

The following is a pictorial representation of the above logic:

C++

#include <iostream>
using namespace std;

// A binary tree structure. 
struct Node {
    int data;
    struct Node *left, *right;
};

// Utility function to create a new node in the Binary Tree.
Node* newNode(int data)
{
    Node* temp = new Node;
    temp->data = data;
    temp->left = nullptr;
    temp->right = nullptr;
    return temp;
}

// A Utility function to print leaf nodes of a given binary tree.
void printLeaves(Node* root)
{
    if (!root)
        return;

    printLeaves(root->left);

    // Print if it is a leaf node.
    if (!(root->left) && !(root->right))
        cout << root->data << " ";

    printLeaves(root->right);
}

// A Utility function to print all the left boundary nodes, except the leaf node. 
// Printng the nodes in Top=down manner.
void printBoundaryLeft(Node* root)
{
    if (!root)
        return;

    if (root->left) {

        // print the node before calling itself for left subtree ensuring top down manner
        cout << root->data << " ";
        printBoundaryLeft(root->left);
    }
    else if (root->right) {
        cout << root->data << " ";
        printBoundaryLeft(root->right);
    }
    // leave leaf node to remove duplicates.
}

// A utility function to print all the right boundary nodes, except the leaf node
// Printing the nodes in BOTTOM UP manner.
void printBoundaryRight(Node* root)
{
    if (!root)
        return;

    if (root->right) {
        // first call for right subtree, after then print this node ensuirng bottom up manner.
        printBoundaryRight(root->right);
        cout << root->data << " ";
    }
    else if (root->left) {
        printBoundaryRight(root->left);
        cout << root->data << " ";
    }
    // leave leaf node to remove duplicates.
}

// Main function to perform boundary traversal of a given binary tree
void printBoundary(Node* root)
{
    if (!root)
        return;

    // Step 1: PRint root node.
    cout << root->data << " ";

    // Step 2: Print the left boundary of the Binary Tree in top-down manner.
    printBoundaryLeft(root->left);

    // Step 3: Print all the leaf nodes
    printLeaves(root->left);
    printLeaves(root->right);

    // Step 4: Print the right boundary of the Binary Tree in bottom-up manner.
    printBoundaryRight(root->right);
}

int main()
{

    Node* root = newNode(1);
    root->left = newNode(2);
    root->left->left = newNode(3);
    root->left->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right = newNode(6);
    root->right->left = newNode(7);
    root->right->right = newNode(8);
           root->right->right->left = newNode(9);
           root->right->right->right = newNode(12);
           root->right->right->left->left = newNode(10);
           root->right->right->left->right = newNode(11);
    printBoundary(root);

    return 0;
}

Output

Time Complexity

The time complexity of the algorithm is O(n) where n is the number of nodes in the binary tree.

As the total time would be a submission of the time taken to perform the above four steps.

1. Time taken to print the root node is - O(1)
2. Time taken to print the left boundary from the top-down is O(n).
3. Time taken to print the leaf nodes In the same sequence as the inorder traversal is O(n).
4. Time taken to print the right boundary from the bottom up is O(n)

where n is defined as the number of nodes in the binary tree.
Space Complexity
The space complexity of the algorithm is O(n) where n is the number of nodes in the binary tree.